In the approach you're considering, you won't have the 'true' PCs unless you're using a synthetic dataset where ground truth is already known.
Reconstruction error is one way to measure performance. In fact, one way to think about PCA is that it minimizes this quantity on the training set. Use PCA to project the points into the low dimensional space. Then, reconstruct the original points by projecting the low dimensional representations back into the original, high dimensional space. The distance between the original points and their reconstructions is inversely related to how well the model captures the structure of the data. This is related to the view of PCA as lossy data compression. When the low dimensional representation retains more information, the original points can be reconstructed more accurately. Reconstruction error can also be used to compute the commonly used performance measure $R^2$ (fraction of variance accounted for).
Cross validation should be used, rather than measuring reconstruction error for the training data. This is because using the training data to both fit the model and measure performance would give an overoptimistic, biased estimate. Instead, cross validation tries to estimate performance on future, unseen data drawn from the same distribution as the training data. Using cross validation, you'd split the data into training and test sets, train the PCA model on each training set, then use it to compute the reconstruction error for the corresponding test set.
The purpose of this quantity is to give a performance metric. But, it's not appropriate to select the number of components by trying to minimize it, because the error decreases with the number of components. This is to be expected, because more information is retained. If the goal is to select the number of components, there are a number of methods to use instead. @amoeba's post here describes how to do this using cross validation.
Computing reconstruction error for the test set
For a particular cross validation fold, say the training set is $X = \{x_1, \dots, x_n\}$, the test set is $X' = \{x'_1, \dots, x'_m\}$, and each point is represented as a column vector. Use the training set to fit the PCA model, consisting of the mean $\mu$, the weights $W$, and the number $k$ of components to retain. If you're using an algorithm to choose $k$, it may differ across training sets (which is ok; what's being tested here is the entire model fitting procedure). If you're also using cross validation to choose $k$, you'd have to split the training set into further training/validation sets (i.e. perform nested cross validation).
To obtain the low dimensional representation $y'$ of a test point $x'$, you'd first subtract the mean, then multiply by the weights:
$$y' = W (x_i' - \mu)$$
To reconstruct the original test point from the low dimensional representation, you'd multiply the low dimensional representation by the transposed weights, then add the mean back again:
$$\hat{x}' = W^T y' + \mu$$
The low dimensional representation discards information, so the reconstruction won't be perfect. Its error can be measured by the squared Euclidean distance between the original test point and the reconstruction:
$$\|x' - \hat{x}'\|^2$$
Therefore, the mean squared reconstruction error for the entire test set is:
$$L(W, \mu, X') =
\frac{1}{m} \sum_{i=1}^m
\left \|x_i' - \left ( W^T W (x'_i - \mu) + \mu \right ) \right \|^2$$
Repeat this procedure for all cross validation folds. Then take the mean reconstruction error across test sets, weighted by the number of points in each test set.
Example plot
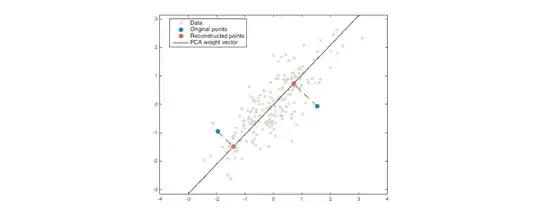
For geometric intuition, here's an example with 2 dimensions and 1 principal component. The grey points are the training data. The blue points are test data, and the orange points are their reconstructions (in practice, there would be many more test points than this). The mean squared reconstruction error is the average squared length of the dashed lines.
Fraction of variance accounted for
$R^2$ (the fraction of variance accounted for) is another way to measure performance. Test set $R^2$ can be computed from the test set reconstruction error:
$$R^2(W, \mu, X') =
1 - \frac{
L(W, \mu, X')
}{
\sum_{i=1}^m \|x'_i - \langle X' \rangle \|^2
}$$
where $\langle X' \rangle$ is the mean of the test set, so the denominator measures the mean squared distance from the test points to their mean (which is equal to the sum of the variance along each dimension).
