What's a good measure of distance between multinomial samples to build a phylogenetic tree?

Question

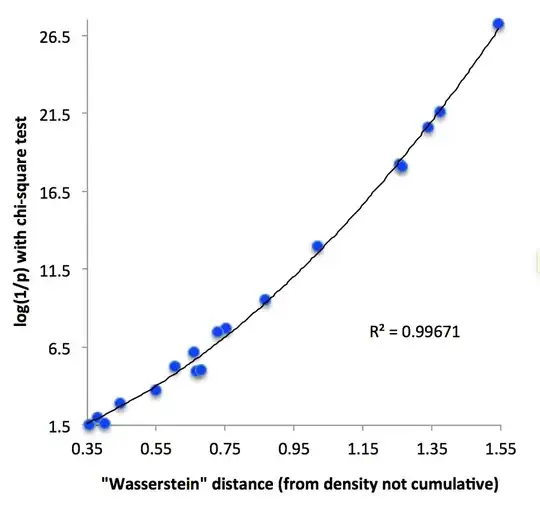
Summary: I'm looking for a measure of distance between multinomial samples of four or more categories in order to build a phylogenetic tree. I considered using log(1/CHI2(sample-1, sample-2)), where CHI2 gives the p-value of the chi-square test between two samples of equal size. I'm not sure whether this makes sense though. What's a good measure of distance between two multinomial samples? Intuitively, I want to be able to say that some sample A is closer to B than to C, then scale this up to thousands of samples to build a phylogenetic tree of sample relatedness.

Archaeologists have long theorised on the relatedness of tool collections coming from different sites, but they rarely use any statistical tests. I'm under the impression that a large number of what they describe as patterns, sometimes on hundreds of pages, is totally spurious. (Besides they might be missing actual patterns.) I am no expert in statistics, but I would be interested in identifying which tool collections --- multinomial samples I believe --- are significantly different from one another, and in quantifying these differences with a measure of distance, eventually to build a phylogenetic tree.

Following one typology (Laplace 1964), there are 85 primary stone tool types, which can be arranged into 14 categories, including for example, that of backed points (pointes à dos):

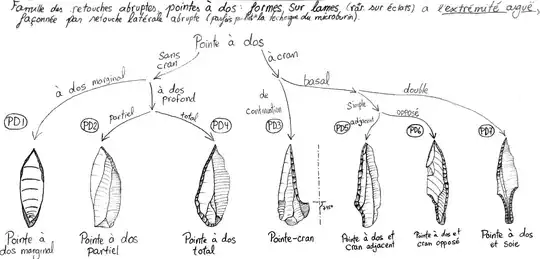
These categories are further arranged into 5 families: Burins (B), Endscrapers (G), tools with abrupt retouch (RA, including backed points), foliaceous ("fancy looking") tools (F), and the substrate (archaic-like, poorly-made tools, S).

To simplify things at first, I want to consider only four tool families (all except the rare F) from eight archaeological layers of the same site.

As a measure of distance between two layers, I tried using log(1/p) where p is the p-value of the two-sample chi-square test. Of course, the p-value depends on sample size, so I eliminated layers with a sample size lower than 200 (layer F) and treated all other layers as if they had a sample size of 214 (the lowest sample size above 200). But is not obvious to me this is the best measure of distance.

How may I get a measure of distance between multinomial samples, ideally without downsizing samples? A distance would have to be symmetric, and to avoid weird behaviour, I'd probably also want dist(sample1, sample3) <= dist(sample1, sample2) + dist(sample2, sample3). I'm aware of this question but am unsure what to do of it.

If I could get a distance function between multinomial samples, my next step would be to build a phylogenetic tree in R using the neighbour joining method.

Answer 1

I ended up using a measure of distance similar to the Wasserstein metric. If the proportion of tools were the following

    Tool type | B    | G    |  T   | DT    | 
 Assemblage A | 0.40 | 0.40 | 0.10 | 0.10  | 
 Assemblage B | 0.25 | 0.25 | 0.25 | 0.25  | 

the Wasserstein metric builds the cumulative frequencies:

    Tool type | B    | B +G |B+G+T |B+G+T+DT| 
 Assemblage A | 0.40 | 0.80 | 0.90 | 1      | 
 Assemblage B | 0.25 | 0.50 | 0.75 | 1      | 

and adds up the absolute column differences: |0.40-0.25| + |0.80-0.50| + |0.90-0.75| + |1-1| = 0.60. This was not ideal, however, as the distance obtained in this way depended on the order of the columns.

I simply used the summed of absolute pairwise differences in the first table. The distance between assemblages A and B is then simply the sum of the absolute values of the differences in relative frequency of each tool type: |0.40 - 0.25| + |0.40 - 0.25| + |0.10 - 0.25| + |0.10 - 0.25| = 0.60.

This distance seemed more natural than the log(1/p) one. In the end the choice of distance did not seem to matter because both measures of distance were highly correlated, which was reassuring: