The problem is from [ISLR][1] Problem 5.R.R2. The data is here.
Consider the linear regression model of $y$ on $X_1$ and $X_2$. Next, plot the data using
matplot(Xy,type="l"). Which of the following do you think is most likely given what you see?
The answer is:
Our estimate of $s.e.(\beta^1$) is too low.
The explanation is:
There is very strong autocorrelation between consecutive rows of the data matrix. Roughly speaking, we have about 10-20 repeats of every data point, so the sample size is in effect much smaller than the number of rows (1000 in this case).
But I could not understand it... According to my opinion, 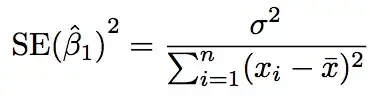 , the denominator of this equation (that used to calculate the estimation of standard error for coefficient) indicates no difference whether xi sequence is autocorrelated or not.
, the denominator of this equation (that used to calculate the estimation of standard error for coefficient) indicates no difference whether xi sequence is autocorrelated or not.