A way of looking at it would be to notice that $Y = U-U'$ with both $U\sim U(0,1)$ and $U'\sim U(0,1)$ follows a standard triangular distribution, which density function is
$$f_Y(y) =
\begin{cases}
y+1, & -1<y<0 \\[2ex]
1-y, & 0<y<1
\end{cases}$$
Here is the plot:
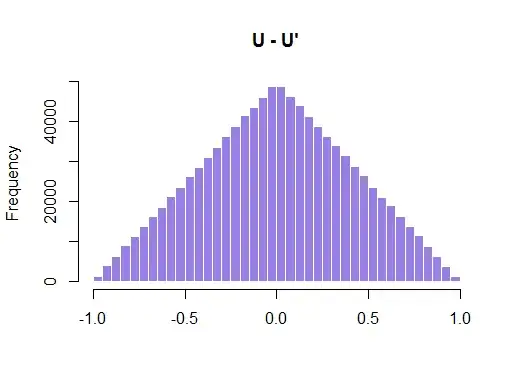
In this way,
$$\text{Var}\left[(U-U')^2\right]=\text{Var}[Y^2]= \mathbb E\left[Y^4\right]-\left[\mathbb E\left[Y^2\right]\right]^2\tag 1$$
Applying LOTUS,
$$\mathbb E[Y^2]=\int_{-1}^0y^2(y+1)\,dy+\int_0^1 y^2(1-y)dy=\frac{1}{6}$$
and
$$\mathbb E[Y^4]=\int_{-1}^0y^4(y+1)\,dy+\int_0^1 y^4(1-y)dy=\frac{1}{15}.$$
Now it's just a matter of plugging these values into $(1).$
Here is the rough-and-tumble reassurance in R:
> set.seed(0)
> u = runif(1e6)
> u_prime = runif(1e6)
> y = u - u_prime
> z = y^2
> mean(z)
[1] 0.166769
> var(z)
[1] 0.03898331
