I am just curious why there are usually only $L_1$ and $L_2$ norms regularization. Are there proofs of why these are better?
-
Proof I don't know, but in practice, lasso in general give better results than ridge due to a better management of the outliers. (and elastic net is the top). I guess regularisation of higher level would struggle to balance outliers. – YCR Mar 23 '17 at 09:47
-
20(+1) I haven't investigated this question specifically, but experience with similar situations suggests there may be a nice qualitative answer: all norms that are second differentiable at the origin will be locally equivalent to each other, of which the $L^2$ norm is the standard. All other norms will not be differentiable at the origin and $L^1$ qualitatively reproduces their behavior. That covers the gamut. In effect, a linear combination of an $L^1$ and $L^2$ norm approximates *any* norm to second order at the origin--and this is what matters most in regression without outlying residuals. – whuber Mar 23 '17 at 14:07
-
@whuber Can I know what do you mean by "norms that are second differentiable at the origin will be locally equivalent to each other, of which L2 norm is the standard"? How does it answer my question? I mean what happens when it is not second differentiable. How can your statement be proven rigorously? – user10024395 Mar 24 '17 at 15:42
-
6Yes: this is essentially Taylor's theorem. – whuber Mar 24 '17 at 15:44
-
4Premise of the question is false: other $\ell_p$-norms are used, albeit much less common. – Firebug Mar 25 '17 at 18:06
-
4The linear combination that @whuber mentions is often called the [elastic net](https://en.wikipedia.org/wiki/Elastic_net_regularization). – Luca Citi Mar 25 '17 at 20:50
-
@whuber Can you provide a reference or explain what you mean? The $L^2$ norm is not differentiable at the origin! – Olivier Mar 26 '17 at 00:48
-
5Also, among Lp norms, $L^\infty$ also gets a lot of mileage. – user795305 Mar 27 '17 at 09:52
-
1The premise of the question is still invalid. You could be asking why we see them more often than others, but I definitely see $\ell_p$-norms with arbitrary $p$ in the literature. I even asked a question about it already: http://stats.stackexchange.com/questions/224531/bridge-penalty-vs-elastic-net-regularization; – Firebug Mar 30 '17 at 16:59
-
@whuber I've included an answer that I think points out a small mistake in thinking of the penalty in the way your comment above does. Specifically, the penultimate paragraph of my answer discusses your comment. I'd greatly appreciate knowing your response to it if you get a chance. – user795305 Jul 03 '17 at 15:05
-
@Ben I read your post yesterday and enjoyed it very much. I apologize for anything that might have been misleading or confusing in the comment--I was trying to convey exactly the point you have made about the differentiability of the level sets of the norms (rather than of the norms themselves). – whuber Jul 03 '17 at 15:10
-
Here is an old similar question with interesting answers: https://stats.stackexchange.com/questions/45643/why-l1-norm-for-sparse-models – kjetil b halvorsen Jul 04 '17 at 18:50
-
this must have something to do with Fermat's theorem – Aksakal Jul 05 '17 at 18:52
-
@whuber Which norm is differentiable at the origin? I don't think any norm is. – 24n8 Jul 10 '20 at 01:03
-
@Iamanon When an $L^p$ norm is used in regularization it is usually in the form of its $p^\text{th}$ power rather than the norm itself. It is in *this* sense that we may consider it (that is, the penalty term) to be differentiable at the origin for $1\lt p\lt\infty.$ I apologize for the misleading language I used in my original comment. – whuber Jul 10 '20 at 12:19
-
1@whuber Ah yes, you're right. I wasn't thinking in terms of the p-th power originally. – 24n8 Jul 10 '20 at 15:26
-
@whuber why is it important to differentiate at the origin? What origin are we even talking about? – Learning stats by example Oct 21 '20 at 00:36
-
@Learning The origin is where the distance is zero. Many optimization algorithms proceed by finding zeros of the derivative, implicitly assuming those are the only places where optima occur--but when a function is not differentiable, other locations (where the derivative fails to exist) are critical points, too, and may be solutions. – whuber Oct 21 '20 at 12:37
3 Answers
In addition to @whuber's comments (*).
The book by Hastie et al Statistical learning with Sparsity discusses this. They also uses what is called the $L_0$ "norm" (quotation marks because this is not a norm in the strict mathematical sense (**)), which simply counts the number of nonzero components of a vector.
In that sense the $L_0$ norm is used for variable selection, but it together with the $l_q$ norms with $q<1$ is not convex, so difficult to optimize. They argue (an argument I think come from Donohoe in compressed sensing) that the $L_1$ norm, that is, the lasso, is the best convexification of the $L_0$ "norm" ("the closest convex relaxation of best subset selection"). That book also references some uses of other $L_q$ norms. The unit ball in the $l_q$-norm with $q<1$ looks like this
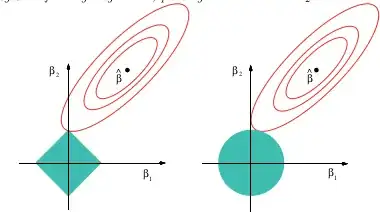
(image from wikipedia) while a pictorial explication of why the lasso can provide variable selection is
This image is from the above referenced book. You can see that in the lasso case (the unit ball drawn as a diamond) it is much more probable that the ellipsoidal (sum of squares) contours will first touch the diamond at one of the corners. In the non-convex case (first unit ball figure) it is even more likely that the first touch between the ellipsoid and the unit ball will be at one of the corners, so that case will emphasis variable selection even more than the lasso.
If you try this "lasso with non-convex penalty" in google you will get a lot of papers doing lasso-like problems with non-convex penalty like $l_q$ with $q < 1$.
(*) For completeness I copy in whuber's comments here:
I haven't investigated this question specifically, but experience with similar situations suggests there may be a nice qualitative answer: all norms that are second differentiable at the origin will be locally equivalent to each other, of which the $L_2$ norm is the standard. All other norms will not be differentiable at the origin and $L_1$ qualitatively reproduces their behavior. That covers the gamut. In effect, a linear combination of an $L_1$ and $L_2$ norm approximates any norm to second order at the origin--and this is what matters most in regression without outlying residuals.
(**) The $l_0$-"norm" lacks homogeneity, which is one of the axioms for norms. Homogeneity means for $\alpha \ge 0$ that $\| \alpha x \| = \alpha \| x \|$.
- 9,773
- 1
- 25
- 51
- 63,378
- 26
- 142
- 467
-
1@kjetilbhalvorsen Thank you for your profound answer. I choose the uncommon superscripting in order to be consistent with the question and the title. Of course you can write it in the way you prefer. – Ferdi Mar 25 '17 at 17:30
-
@kjetilbhalvorsen Can you expand a little on Whuber's comment? It is well known that the $L^2$ norm is not differentiable at the origin (consider $x \mapsto |x|$, for instance). It is not clear either what is meant by 'local equivalence' of norms. References are needed, to say the least. – Olivier Mar 26 '17 at 19:02
-
@Olivier The $\ell_2$-norm is differentiable at the origin, you are thinking about the $\ell_1$-norm. – Firebug Mar 27 '17 at 11:59
-
@Firebug No. I'm thinking about the $L^2$ norm in 1 dimension, which is there the same as the $L^1$ norm. Am I missing something? – Olivier Mar 27 '17 at 12:38
-
2@Olivier Oh, you are actually right. I misunderstood, because the squared $\ell_2$-norm is actually used, and it's differentiable everywhere. – Firebug Mar 27 '17 at 12:40
-
@Firebug Yet the mathematical mumbo-jumbo in whuber's comment has not been corrected... – Olivier Mar 27 '17 at 22:42
-
I think I ask in the question for proofs rather than qualitative answer. Is there a reason why almost everyone is giving me qualitative answers? – user10024395 Mar 28 '17 at 17:45
-
It isn't very clear what you want proved ... (will look into it, but now I am travelling ...) – kjetil b halvorsen Mar 28 '17 at 18:09
-
@Olivier Well, referring to $\|\cdot\|_2^2$ as the $\ell_2$-norm is so commonplace in practice and in the literature we sometimes forget it was actually squared to begin with, don't be harsh. – Firebug Mar 30 '17 at 16:57
I think the answer to the question depends a lot on how you define "better." If I'm interpreting right, you want to know why it is that these norms appear so frequently as compared to other options. In this case, the answer is simplicity. The intuition behind regularization is that I have some vector, and I would like that vector to be "small" in some sense. How do you describe a vector's size? Well, you have choices:
- Do you count how many elements it has $(L_0)$?
- Do you add up all the elements $(L_1)$?
- Do you measure how "long" the "arrow" is $(L_2)$?
- Do you use the size of the biggest element $(L_\infty)$?
You could employ alternative norms like $L_3$, but they don't have friendly, physical interpretations like the ones above.
Within this list, the $L_2$ norm happens to have nice, closed-form analytic solutions for things like least squares problems. Before you had unlimited computing power, one wouldn't be able to make much headway otherwise. I would speculate that the "length of the arrow" visual is also more appealing to people than other measures of size. Even though the norm you choose for regularization impacts on the types of residuals you get with an optimal solution, I don't think most people are a) aware of that, or b) consider it deeply when formulating their problem. At this point, I expect most people keep using $L_2$ because it's "what everyone does."
An analogy would be the exponential function, $e^x$ - this shows up literally everywhere in physics, economics, stats, machine learning, or any other mathematically-driven field. I wondered forever why everything in life seemed to be described by exponentials, until I realized that we humans just don't have that many tricks up our sleeve. Exponentials have very handy properties for doing algebra and calculus, and so they end up being the #1 go-to function in any mathematician's toolbox when trying to model something in the real world. It may be that things like decoherence time are "better" described by a high-order polynomial, but those are relatively harder to do algebra with, and at the end of the day what matters is that your company is making money - the exponential is simpler and good enough.
Otherwise, the choice of norm has very subjective effects, and it is up to you as the person stating the problem to define what you prefer in an optimal solution. Do you care more that all of the components in your solution vector be similar in magnitude, or that the size of the biggest component be as small as possible? That choice will depend on the specific problem you're solving.
The main reason for seeing mostly $L_1$ and $L_2$ norms is that they cover the majority of current applications. For example, the norm $L_1$ also called the taxicab norm, a lattice rectilinear connecting norm, includes the absolute value norm.
$L_2$ norms are, in addition to least squares, Euclidean distances in $n$-space as well as the complex variable norm. Moreover, Tikhonov regularization and ridge regression, i.e., applications minimizing $\|A\mathbf{x}-\mathbf{b}\|^2+ \|\Gamma \mathbf{x}\|^2$, are often considered $L_2$ norms.
Wikipedia gives information about these and the other norms. Worth a mention are $L_0$. The generalized $L_p$ norm, the $L_\infty$ norm also called the uniform norm.
For higher dimensions, the L$_1$ norm or even fractional norms, e.g., L$_\frac{2}{3}$ may better discriminate between nearest neighbors than the $n$-space distance norm, L$_2$.
- 11,532
- 7
- 45
- 102