I'm not sure the best way to word this question, so excuse my ignorance.
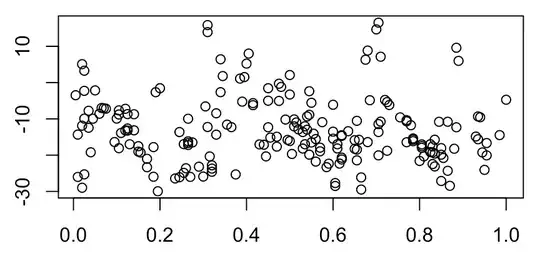
I'm working with some data that I am expecting to contain around three or four peaks or troughs:
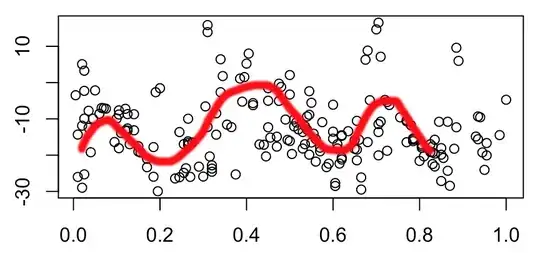
I am pleased to note that the data appear to contain the wiggle I expected, which I have roughly superposed (hand-drawn) here:
I am able to make some predictions regarding the number of zero-crossings (three, or maybe four). I also am able to make some guesses at where I'd expect these to be. I'd like to keep as many of these assumptions free as possible, but can bring in these constraints to build a model if necessary.
I'm looking for a statistical test that will tell me if the data truly are 'wiggly', and ideally, would like to find the zero crossings. I recognise that this will involve playing with a few parameters (or perhaps fixing them according to my predictions), but am currently unsure where to begin in doing this.
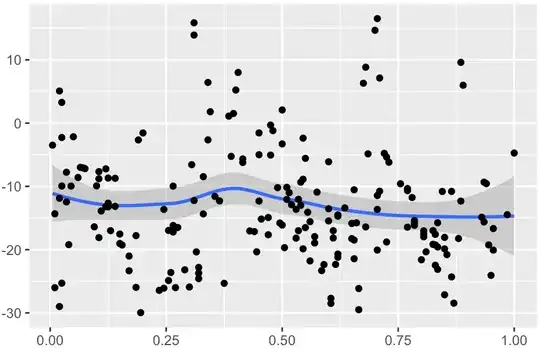
An attempt to fit a LOESS local regression results in the following:
I know that I could fiddle with the parameters until I make something fit, but I'd like to know the best way of doing this sensibly, and crucially, being able to state clearly that the pattern I'm seeing is real (albeit with a lot of noise). Perhaps this will involve building a model and then checking how well it fits the data.
Any suggestions for the sorts of techniques I could use would be appreciated. I understand that this is likely to involve some form of Time Series Analysis techniques, but due to the lack of an explicit periodicity, I'm not sure if that's entirely appropriate.
Here are the data in a form that can be imported into R:
dat <- structure(list(x = c(0.005, 0.01, 0.01, 0.02, 0.02, 0.02, 0.025,
0.025, 0.025, 0.025, 0.035, 0.035, 0.04, 0.045, 0.05, 0.06, 0.065,
0.07, 0.075, 0.095, 0.1, 0.105, 0.105, 0.105, 0.11, 0.12, 0.12,
0.125, 0.125, 0.125, 0.13, 0.14, 0.14, 0.15, 0.15, 0.155, 0.17,
0.17, 0.185, 0.185, 0.19, 0.195, 0.2, 0.235, 0.245, 0.245, 0.255,
0.255, 0.26, 0.265, 0.265, 0.265, 0.265, 0.27, 0.275, 0.29, 0.3,
0.305, 0.31, 0.31, 0.31, 0.315, 0.32, 0.32, 0.32, 0.33, 0.33,
0.34, 0.34, 0.345, 0.355, 0.365, 0.375, 0.385, 0.39, 0.395, 0.4,
0.405, 0.415, 0.415, 0.43, 0.44, 0.445, 0.45, 0.45, 0.45, 0.455,
0.47, 0.47, 0.475, 0.475, 0.48, 0.49, 0.495, 0.5, 0.5, 0.5, 0.505,
0.51, 0.51, 0.515, 0.52, 0.53, 0.53, 0.535, 0.535, 0.54, 0.54,
0.545, 0.545, 0.545, 0.55, 0.55, 0.555, 0.56, 0.56, 0.57, 0.57,
0.575, 0.585, 0.59, 0.6, 0.6, 0.6, 0.605, 0.605, 0.61, 0.61,
0.615, 0.62, 0.62, 0.62, 0.62, 0.635, 0.65, 0.65, 0.655, 0.655,
0.655, 0.66, 0.665, 0.665, 0.675, 0.68, 0.68, 0.685, 0.7, 0.705,
0.705, 0.705, 0.705, 0.71, 0.71, 0.72, 0.725, 0.725, 0.73, 0.755,
0.77, 0.77, 0.77, 0.78, 0.785, 0.785, 0.785, 0.8, 0.805, 0.805,
0.805, 0.81, 0.825, 0.825, 0.83, 0.83, 0.83, 0.835, 0.835, 0.835,
0.845, 0.85, 0.85, 0.85, 0.855, 0.865, 0.865, 0.87, 0.88, 0.885,
0.885, 0.89, 0.93, 0.935, 0.935, 0.94, 0.945, 0.95, 0.955, 0.955,
0.985, 1), y = c(-3.484848485, -14.33333333, -26.01010101, -11.88016529,
5.075757576, -28.98550725, -2.279957582, 3.26953748, -25.3030303,
-9.94531784, -12.45284186, -7.765616857, -19.21387791, -9.956709957,
-2.157738095, -8.596837945, -6.994849683, -7.070707071, -7.196969697,
-16.39118457, -9.924242424, -8.793706294, -7.662337662, -18.0952381,
-13.88888889, -13.19444444, -7.231404959, -8.683982684, -13.23076923,
-12.65477354, -16.99976625, -8.722222222, -13.16137566, -19.03053087,
-17.53472222, -19.26736881, -21.01449275, -23.33333333, -17.78390805,
-25.95818815, -2.660105548, -29.95495495, -1.550497866, -26.43467643,
-26.09302326, -13.63636364, -16.96521869, -24.88005997, -23.61078819,
-16.18135626, -17.21088435, -16.66666667, -9.964012596, -26,
-16.50219298, -23.1884058, -25.9, -6.566985646, -12.23958333,
15.85526316, 13.91304348, -20.35573123, -22.81329781, -23.71541502,
-24.57873934, -8.465608466, -14.35786436, 6.428571429, -2.651515152,
1.797385621, -11.58963585, -12.28475228, -25.31931932, 1.0998011,
-5.257936508, 1.520608243, 5.22875817, 8, -6.225895317, -5.663587749,
-17.04545455, -17.13842975, -20.34574468, -5, -12.31884058, -1.551226551,
-15.16312057, -14.92144026, -17.65005828, -0.310800311, -5.050505051,
-1.198801199, -10.19345238, -15.78947368, -16.11842105, -3.289473684,
2.083333333, -19.6827262, -12.06913435, -10.14739229, -10.995086,
-12.89146289, -13.63636364, -18.18181818, -12.0414673, -17.003367,
-9.339774557, -12.99302549, -19.86504279, -2.380952381, -8.873307544,
-16.51469098, -5.568181818, -14.08948195, -15.57002111, -21.78017241,
-18.9484127, -17.93478261, -10.91269841, -23.31492984, -22.35449735,
-15.45729403, -13.53383459, -6.111111111, -28.5, -27.69423559,
-17.00626959, -18.15942678, -22.33635929, -14.51133408, -20.6915564,
-14.69979296, -21.19883041, -13.40136054, -15.86466165, -18.25657895,
-18.48103372, -21.43438572, -10.53846154, -15.75833333, -26.14583333,
-29.49002217, 6.297117517, -16.40977444, 8.829365079, -4.861111111,
14.66303966, -20.06514165, -13.63636364, -11.44661408, 16.51515152,
-10.76388889, 7.126322751, -4.783549784, -18.79002359, -5.370985604,
-6.186868687, -9.588675214, -10.67725753, -10.35196687, -16.44736842,
-11.76201373, -15.72617946, -16.15516871, -15.3968254, -21.6,
-17.96831956, -17.02792299, -17.5, -20.34090909, -19.16076845,
-16.99083862, -22.4627451, -17.586727, -19.24242424, -23.11827957,
-19.58064516, -15.74898785, -10.80586081, -18.06375443, -27.13316096,
-19.87394958, -20.77922078, -10.79633056, -24.30992808, -28.45564516,
-18.24229692, -12.32492997, 9.598930481, 5.980861244, -14.87414188,
-15.6213705, -9.329798515, -9.565217391, -19.25465839, -24.06204906,
-20.07407407, -16.66666667, -14.47596533, -4.73172988)), .Names = c("x",
"y"), class = "data.frame", row.names = c(NA, -200L))