Effect of exp(ϵ) in Differential Privacy Definition

Question

I am reading about differential privacy and would like to understand the implications of the different values of $\varepsilon$ in the definition below:

$$\mathbb{P}[K(D_1) \in \mathcal{S}] \leqslant \exp(\varepsilon) \times \mathbb{P}[K(D_2) \in \mathcal{S}]$$

What would $0 < \varepsilon < 1$, $\varepsilon > 1$ , $\varepsilon > 10$ , etc mean in terms of preserving privacy?

Answer 1

The following graph quantifies the amount of information that a Bayesian attacker can gain after seeing the result of an $\varepsilon$-differentially private algorithm, for different values of $\varepsilon$. The $x$-axis is the prior that the attacker has on some property of their target user, and the $y$-axis is the posterior.

This answers your question somewhat:

• If $\varepsilon$ is very close to $0$, an attacker gains almost no information.
• For $\varepsilon=1$, an attacker which starts with a prior of 50% can at most increase it to 66%.
• For $\varepsilon=7$, the privacy level is already very low: in the worst case, even an attacker with a small prior knowledge 5% can increase it to more than 95%.

The blog post that the graph is taken from explains this in more detail.

Answer 2

A smaller $\epsilon$ indicates better differential privacy. Indeed, by swapping $D_1$ and $D_2$ you see $\epsilon$-DP implies $$ e^{-\epsilon} \mathbb{P}(K(D_2) \in S) \le \mathbb{P}(K(D_1) \in S) \le e^{\epsilon} \mathbb{P}(K(D_2) \in S). $$ The limiting $\epsilon \to 0$ case of this is $\mathbb{P}(K(D_1) \in S) = \mathbb{P}(K(D_2) \in S)$, i.e. the scheme is perfect statistically.

The practical level of privacy offered for higher $\epsilon$ depends on the application. For most applications though ($\epsilon=10$)-DP wouldn't be worth much! (e^{-10} = 0.000045..)

Answer 3

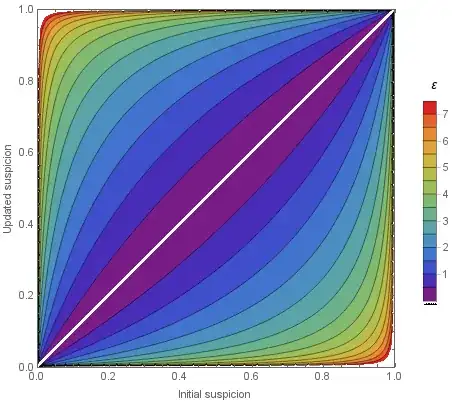
Some insight can be gained with basic algebraic manipulation of the inequality. Re-arranging gives:

$$\ln \mathbb{P}(K(D_1) \in \mathcal{S}) - \ln \mathbb{P}(K(D_2) \in \mathcal{S}) \leqslant \varepsilon.$$

Under $\varepsilon$-differential privacy, this inequality holds over all data sets $D_1$ and $D_2$ that differ by only one element, and all sets $\mathcal{S}$. Thus, we can see that $\varepsilon$ represents an upper bound on the logarithmic difference between the probabilities of the events $K(D_1) \in \mathcal{S}$ and $K(D_1) \in \mathcal{S}$. That is, under $\varepsilon$-differential privacy the value $\varepsilon$ gives an upper bound on the logarithmic difference between the probabilities that the algorithm output of two similar data sets (differing by one element) fall within any set. So the relevant ranges you are specifying for this value are giving ranges of values for upper bounds on this logarithmic difference.