3

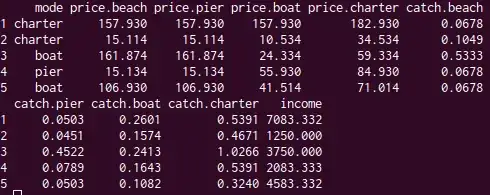
When we calculate the total contribution of a variable for a single dimension, the sum of all single contributions is equal to 100%, which makes perfect sense.

The http://www.sthda.com suggests to calculate the total contribution of a variable for several dimensions multiplying single contributions to their eigenvalues, i.e.

(C1 * Eig1) + (C2 * Eig2) +...+ (Cn * Eign)
where Eig - the eigenvalues

-the total sum of all contributions is more than 100%. See the example here - chart "Contribution of variables to Dim 1-2":

enter image description here

I am confused here... Let's say the contributions of three variables on Dimensions from 1 to 5 are 97%, 91% and 85% respectively. My question: how should we interpret variable contributions to several dimensions?

user2723490
  • 241
  • 1
  • 4
  • 6
  • Two things... Can you post (giving credit to the authors) the plots or charts you are referring to? Also, and without getting into details, notice that the contributions of the PCA are orthogonal, while the actual variables are not. – Antoni Parellada Mar 16 '17 at 00:30
  • See the chart. I guess the correct way of calculating % of multi-dimensional contributions should be by dividing them by their total sum - not the formula given in http://www.sthda.com. – user2723490 Mar 16 '17 at 00:38
  • You may find [this post](http://stackoverflow.com/a/12760337/4089351) useful from a practical standpoint. Otherwise, and regarding the $>100\%$ issue, I would highly recommend you a [post in our SE.CV community](http://stats.stackexchange.com/a/179042/67822), where a baboon face is PCA decomposed (via SVD), and reflect on the fact that different parts of the anatomy of the face are reflected in multiple singular values. – Antoni Parellada Mar 16 '17 at 00:47
  • 1
    Contribution of a variable into a dimension in PCA is the eigenvector value squared http://stats.stackexchange.com/a/143949 – ttnphns Mar 16 '17 at 10:46

0 Answers0