Finding the probability of getting a complete set from N classes of objects in M draws

Question

Possible Duplicate:
What is the probability of n people from a list of m people being in a random selection of x people from a list of y people?

Let's say we have 5 kinds of marbles, 1000 of each, mixed up in a giant tub. I want to know how many I have to draw out (without replacement) before I can be 50/70/90% sure I have at least 1 of each type of marble.

I can write a script to compute every possibility in M draws for M=5 to 4001, and get the probability from that, but (my point is) I figure there must be a statistical distribution that handles this more directly. Is there a name for such a distribution?

Also, if the counts are not equal (i.e. 100 of type 1, 300 of type 2, ...), is there a distribution that handles that?

Answer 1

I am unaware of a name for this distribution, but the probabilities are straightforward to work out. Not by computing all possible draws, though! (There are far too many.)

The technique is quite general, so let's broaden the problem statement. Suppose we have $n_i \gt 0$ marbles of color $j$, $j=1,2,\ldots,l$, for a total of $n=n_1+\cdots +n_l$ marbles. For any subset of these colors $J = \{j_1,\ldots,j_s\}$, what fraction of all simple random samples of size $k$ contain exactly these colors? The answer is immediate: it's the number of all simple random samples of size $k$ from a bag containing only marbles whose colors are in $J$, divided by the number of all simple random samples of size $k$ from the original bag:

$$f(J, k) = \binom{n_{j_1}+n_{j_2}+\cdots+n_{j_s}}{k} / \binom{n}{k}$$

By the Principle of Inclusion-Exclusion, the fraction of simple random samples of size $k$ without all $l$ colors equals

$$\sum_{\varnothing \ne J \subset \{1,\ldots,l\}}(-1)^{l-\vert J\vert}f(J,k).$$

The computational effort, properly coded, is $O(2^l)$--fine for small numbers of distinct colors--and just $O(l)$ when all the $n_i$ are equal, because all terms for $J$ of a given size will be equal and only sizes $1$ through $l$ need be considered. A Mathematica program that directly expresses the general formula is

h[x_, k_Integer] /; Total[x] >= k > 0 := 
With[{n = Total[x], l = Length[x]},
  Sum[(-1)^(l - j) Binomial[m, k]/Binomial[n, k], {j, 1, l}, {m, Total /@ Subsets[x, {j}]}]
]

Using it, it takes 0.015 seconds (on one core) to find h[{1000,1000,1000,1000,1000}, k] for k from 5 through 34. Rounded, the values are

0.038, 0.115, 0.215, 0.323, 0.428,     0.523, 0.607, 0.679, 0.739, 0.789,
0.83,  0.863, 0.89,  0.912, 0.929,     0.943, 0.955, 0.964, 0.971, 0.977, 
0.981, 0.985, 0.988, 0.991, 0.992,     0.994, 0.995, 0.996, 0.997, 0.998 

Here is a plot of these values:

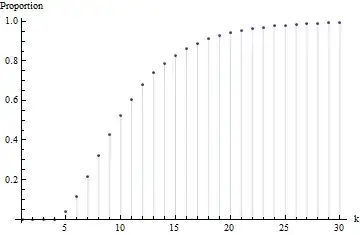
For instance, the chance that all five colors are obtained in the first five draws is $.038 = 3.8\%$ (more precisely, it's $0.038476...$). As a check, if the sampling were with replacement this chance wouldn't change much and it would be computed as $1 \times \frac{4}{5} \times \frac{3}{5} \times \frac{2}{5} \times \frac{1}{5} = 0.0384$.

By inspection, the answer to the question (concerning the 50%/70%/90% points) is $10, 13, 18$. For instance, $k=17$ draws have less than a 90% chance of exhibiting all five colors (the chance is $0.89$) while $k=18$ draws have at least a 90% chance (it's actually $0.912$).

Answer 2

An asympotic approximation - considering that the number of balls is quite large.

We have $l$ types of balls, $n_i$ of each them for a total of $n_1 + \cdots +n_l=n$ (in the example, $l=5$, $n_i=1000$, $n=5000$). Let's call $x_i$ the number of balls of type $i$ that result selected in $k$ extractions. For large $n$, the $x_i$ can be approximated as independent Poisson variables with mean $\lambda_i = k \frac{ni}{n}$

We are interested in the probability that all them are greater than zero, say $P(k)$. In this approximation:

$$P(k) \approx \prod_{i=1}^l \left( 1- e^{-\lambda_i}\right) = \prod_{i=1}^l \left( 1- \exp\left(- k \frac{n_i}{n}\right)\right) $$

and if $n_i = n_1 $ we have $$P(k)=\left( 1- \exp\left(- k \frac{n_1}{n}\right)\right)^l$$

or $$ k = - \frac{n}{n_1} \log\left(1-P(k)^{1/l}\right)$$

In our example, this gives, for $P(k) =$ 0.5, 0.7, 0.9, the values $k \approx$ 10, 13, 19