4

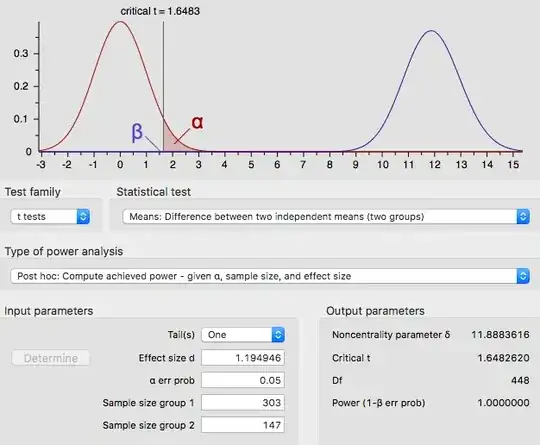
I'm using a program called GPower to calculate the achieved power of a certain test I've performed. Below is the screen shot of my inputs and outputs.

enter image description here

It states that my test achieved a power of 1.0 - meaning there is a ZERO percent chance of a Type II error occurring. I've never seen it described in this way before, just as I've never seen a p-value = 0 (although I'm aware this can happen under extreme circumstances). Is this answer correct, and if so, how can a test be so confident in its results?

Nicholas Hassan
  • 247
  • 1
  • 6

2 Answers2

8

  1. The answer to the title question is "yes", there are hypothesis tests that have alternatives with power 1 (where under that specific alternative you will reject the null with certainty). Consider, for example, a Kolmogorov-Smirnov test of U(0,1) at say n=50 (or pick any other sample size large enough to do the test), where the data are actually from a U(1,2); there's no chance it won't reject.

  2. However, in the case you're looking at, the answer is "no". The power there isn't literally 1, it's strictly less than 1.

  3. The reason it looks like it's 1 when it isn't is simply rounding/truncation error. You have a result displayed to a finite number of places, and the nearest representable number in that many figures to the thing it calculated can be 1.000... (it only shows about 8 there).

    This happens easily if the effect size is large (nearly 12 standard errors? Large). In fact, it can easily be 1 to more figures than the computer holds (i.e. it can be that even the internal representation of the power calculates to 1 even though the thing it's trying to calculate isn't. The type II error rate can be clearly non-zero but when you subtract that from 1. you can get 1.000... not just to 8 digits in the display there, but to all the figures the computer uses to represent the number. The effect size here is so large, this will actually be the case for your computation unless you're using around 100 binary digits -- for example quad precision should be enough to tell it from 1; you need close to 100 digits to represent the number distinct from 1 and IEEE 754 binary128 has about 113, so as long as there's not substantial loss of precision in getting to the 11.8 whatever number that should do. I bet the software isn't using that much precision though. )

Community
  • 1
Glen_b
  • 257,508
  • 32
  • 553
  • 939
1

That's what I get with my Excel sheet to calculate power as well. In Excel, that's due to the fact that t is only calculated up to some large/small probability level. The reality is, that the power is very, very close to 1.

Note in your graph that the distributions don't overlap at all.

zbicyclist
  • 3,363
  • 1
  • 29
  • 34
  • Thanks, it's nice to have some confirmation. I guess I'm just surprised to see that the test was so powerful that the program would be willing to round up to 1 – Nicholas Hassan Mar 13 '17 at 00:39