what is the meaning of 'normality' as a difference between parametric and nonparametric method?

Question

I'm so confused of the definition of the terminology, "normality". I mean, normality of what?

According to central limit theorem, regardless of the distribution of population,the computed values of the average will be distributed according to the normal distribution, which allows us to do statistical analysis.

However, lots of sources of information say that in order to do the parametric method which includes most of the statistical analysis we conduct, the data should follow normal distribution.

In my view at this point, tho arguments don't agree, and they contradicts to each other.

I want to specify the term, 'normality' of data.

Answer 1

Parametric methods simply mean we assume a distribution with some fixed number of parameters (usually unknown). The normal distribution is very common, but there' many other possibilities such as binomial distribution. It doesn't mean your data is actually normally distributed, just that you assume normality is a good assumption for your data.

You certainly don't need to assume your data come from a normal distribution to do parametric methods (e.g: logistic regression). As you study more into statistics, you'll know most statistical methods actually don't require normality.

CLT is a statement about arithmetic means for large sample size - you can approximate it with a normal distribution. It tells you nothing about parametric or non-parametric method.

However, some statistical methods such as t-test use CLT to derive test statistics for the null hypothesis.

Answer 2

I'm so confused of the definition of the terminology, "normality". I mean, normality of what?

Normality refers to some random variable having a normal distribution.

This specifies a particular functional form for the density (and for the distribution function, and for the MGF and the characteristic function, and so on)

Be warned -- many things that look roughly normal are not, and some can have behavior that's quite different from that of the normal distribution.

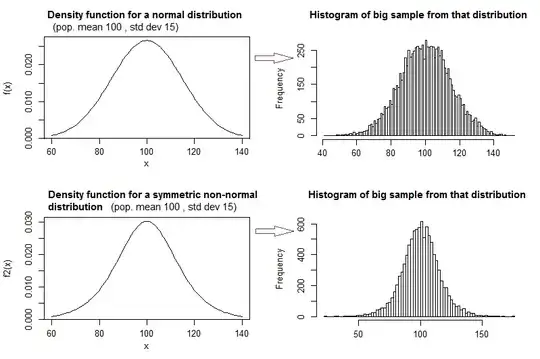
According to central limit theorem, regardless of the distribution of population,the computed values of the average will be distributed according to the normal distribution,

That's not quite what the central limit theorems (any of them) say. However, distributions of sample averages do indeed often tend to be close to normally distributed (without the population distribution of those averages actually being normally distributed)

which allows us to do statistical analysis.

Well, no, that's not right. We don't need normal distributions to do statistical analysis at all. For example I can say "my model for these waiting times is exponential" and do statistical analysis on that basis.

Or I might make no distributional assumption at all and still carry out a statistical test (e.g. I could construct a test for comparing means, if I wanted, without assuming any particular functional form for the distribution function) --- or I could construct an interval for a difference in means, or a number of other things. If I want to fit and test a linear relationship between two variables I can do that without assuming normality (and indeed without using least squares); all manner of statistical analysis -- parametric and nonparametric doesn't need to even consider whether a distribution might be normal. Maybe it is, maybe it isn't, but that's not remotely essential to being able to perform statistical analysis.

Some commonly taught things do rely more or less on assuming normal distributions, but plenty of things would work just fine without it.

However, lots of sources of information say that in order to do the parametric method which includes most of the statistical analysis we conduct, the data should follow normal distribution.

That's just wrong. "Parametric" doesn't imply normality at all. Many of the most widely used methods use normal assumptions but there's no suggestion that being parametric means normal. It means having a fixed, finite number of parameters (as opposed to nonparametric which doesn't have a fixed, finite number of parameters).

For example that exponential model I mentioned above is parametric:

In this case the distribution has one parameter, related to its mean.

(... as is the non-normal symmetric distribution I showed before; as it happens, that one is logistic and has two parameters)

I want to specify the term, 'normality' of data.

Data are not normal (strictly speaking). Our model for the distribution of the population from which our data were drawn may sometimes be normal, but as Box's famous quote says, all models are wrong. A wisely-chosen model may still be highly useful.

A sample may sometimes be reasonably consistent with having been drawn from a normal distribution. We might then use a kind of verbal shorthand and say "the data look close to normal", but we really mean that it looks like it's more or less consistent with having come from a population whose distribution is normal.