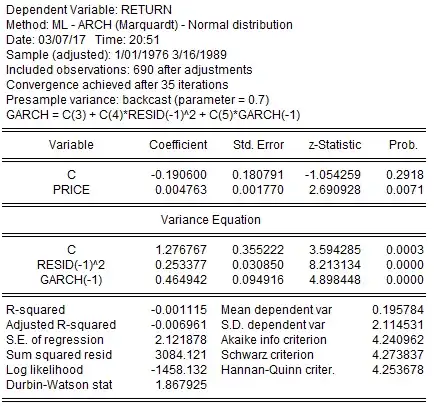
I have a time series that has at least an ARCH(1) process in the error. The model is:
ŷ = β0 + β1*x + ARCH + e
In other words, a constant, 1 independent variable and an ARCH term and the errors.
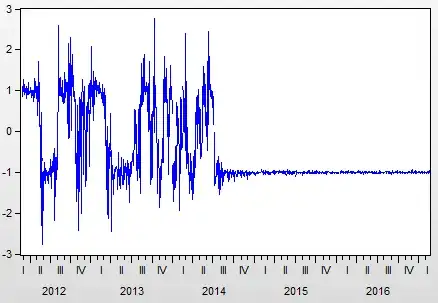
I have the following residual plots. The first in level form:
And standardized:
The second portion of the data set seem to be stationary when transformed into standardized errors, however the first portion has clear periodicity. Assuming that there is no specification error in the theory of my model (big assumption right?), but instead postulating between the following:
- Could my ARCH process be of the wrong order? Mine is simply ARCH(1)
- Or should I transform my variables? Currently they are in level form. I did try log form, but both residuals plots still came out the same. I did not try first differencing yet.
If there is another explanation, please share. I feel there are many diagnostic approaches and it's a little overwhelming. My hope is that within the resid plots above there is a sign of sorts that I have missed and perhaps those with more experience will notice.