10

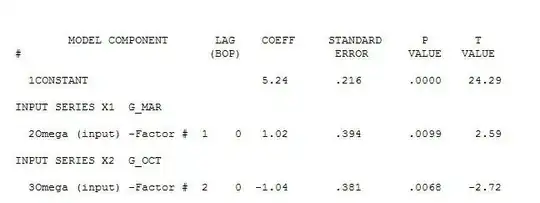
From Wikipedia: https://en.wikipedia.org/wiki/Residual_sum_of_squares, the RSS is the average squared error between true value $y$, and the predicted value $\hat y$.

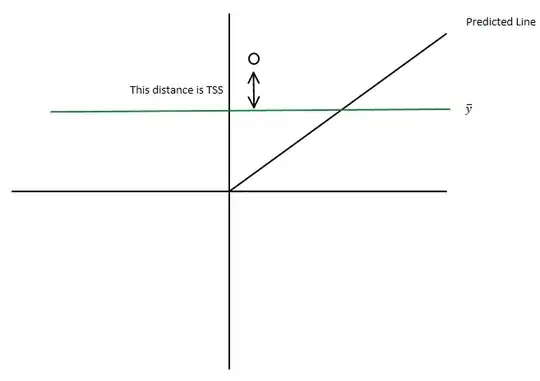
Then according to: https://en.wikipedia.org/wiki/Total_sum_of_squares, the TSS is the squared error between the true value $y$, and the average of all $y$.

However, I don't understand this line under the explanation for TSS:

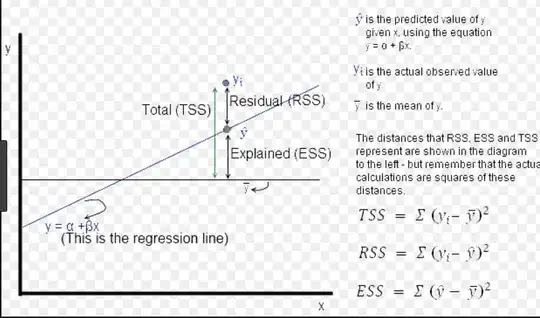
[...] the total sum of squares equals the explained sum of squares plus the residual sum of squares.

If we plot RSS on the graph, it would look like:

enter image description here

TSS Plot:

enter image description here

ESS Plot:

enter image description here

According to the images, the residual (unexplained) value is actually larger than the TSS. Is there something I'm not following?

Stefan
  • 4,977
  • 1
  • 18
  • 38
user1157751
  • 517
  • 1
  • 6
  • 17
  • 4
    That's why the summation is important. As to why you can partition it see http://stats.stackexchange.com/questions/258284/linear-regression-why-can-you-partition-sums-of-squares/258308#258308 – Łukasz Grad Mar 06 '17 at 23:20
  • @ŁukaszGrad, I looked at the post and unfortunately I don't really get it. Can you elaborate a bit further? Thanks – user1157751 Mar 06 '17 at 23:24
  • 2
    This may also help you: http://stats.stackexchange.com/questions/256726/linear-regression-what-does-the-f-statistic-r-squared-and-residual-standard-err/256821#256821 and this perhaps too: http://stats.stackexchange.com/questions/255973/why-do-the-anova-assumptions-equality-of-variance-normality-of-residuals-matt/256104#256104 And maybe this one: http://stats.stackexchange.com/questions/256344/why-is-correlation-not-very-useful-when-one-of-the-variables-is-categorical/256380#256380 – Stefan Mar 06 '17 at 23:25

2 Answers2

10

You have the total sum of squares being $\displaystyle \sum_i ({y}_i-\bar{y})^2$

which you can write as $\displaystyle \sum_i ({y}_i-\hat{y}_i+\hat{y}_i-\bar{y})^2 $

i.e. as $\displaystyle \sum_i ({y}_i-\hat{y}_i)^2+2\sum_i ({y}_i-\hat{y}_i)(\hat{y}_i-\bar{y}) +\sum_i(\hat{y}_i-\bar{y})^2$ where

  • the first summation term is the residual sum of squares,
  • the second is zero (if not then there is correlation, suggesting there are better values of $\hat{y}_i$) and
  • the third is the explained sum of squares

Since you have sums of squares, they must be non-negative and so the residual sum of squares must be less than the total sum of squares

Henry
  • 30,848
  • 1
  • 63
  • 107
  • Hi, thanks for your answer. It may be a bit too late, but can you elaborate on how the 2nd term means mathematically? Looking at the equation, I don't think I can come up with the conclusion that it needs to be 0. Thanks again! – user1157751 Mar 09 '17 at 07:50
  • Can I say this for the second term: For linear regression, the amount we over estimate and under estimate is zero, so when we sum $y_i$-$\hat y_i$, we will get 0? – user1157751 Mar 09 '17 at 18:29
  • Yes you should get $0$ since the average of each should be $\bar{y}$ and so they have the same sums. But my point is subtly different: the residuals should be uncorrelated with the predicted values as a direct result of the linear regression – Henry Mar 09 '17 at 18:35
  • Thanks for your reply again! I don't see a connection between "the residuals should be uncorrelated with the predicted values as a direct result of the linear regression" with any of the terms (1, 2, and 3). Can you give me some hints? Thanks – user1157751 Mar 09 '17 at 18:44
  • 2
    $\sum_i ({y}_i-\hat{y}_i)(\hat{y}_i-\bar{y})$ is the covariance of the residuals and the predicted values. Try an ordinary least squares regression and see that it is zero – Henry Mar 09 '17 at 21:15
  • Do you mean $cov((y_i- \hat y_i), \hat y_i)$? Thanks again, I'm trying to work out the math details to fully understand what is going on. – user1157751 Mar 09 '17 at 21:43
4

This chart was very helpful for me. enter image description here

Via

Learning stats by example
  • 211
  • 4
  • 17