How can I simulate from the density $f(x)=x^2\phi(x)$? Where $\phi$ is the standard normal density. Preferably directly, without using MCMC.
-
4Could you provide more details on where you are stuck? This is a simple density for which standard methods like accept-reject or ratio of uniform work. – Xi'an Mar 05 '17 at 09:27
-
@Xi'an I was just thinking that there might be a magic trick to simulate directly from this distribution without having to go for less efficient methods. – Patel Mar 05 '17 at 09:30
-
2accept-reject and ratio of uniform algorithms are "efficient" enough to be the methods behind the standard simulators for most classical distributions. – Xi'an Mar 05 '17 at 09:37
-
@Xi'an Yes! But not as efficient as direct simulation! – Patel Mar 05 '17 at 11:21
-
@Glen_b In my case, I just need to be able to simulate from that distribution. An efficient method is desirable. – Patel Mar 05 '17 at 11:32
-
@Glen_b Because I am going to simulate it many times, plug the values into a model, and then repeat it many times (a Monte Carlo simulation). Thus, the efficiency requirement. The method in your answer looks great, I just need to check how to simulate from $X^2/2$. – Patel Mar 05 '17 at 11:34
-
Is the project related to your education in some way? – Glen_b Mar 05 '17 at 11:37
-
@Glen_b Yes, it is. I need to do a simulation study for a project and I came across this problem. Although I can use a inverse transform sampling method, I was looking for something faster. – Patel Mar 05 '17 at 11:38
-
Rejection-sampling is very fast and efficient. It can be done in multi-core. I don't see any reason why you wouldn't do that. – SmallChess Mar 05 '17 at 11:42
-
Comments are not for extended discussion; part of this conversation has been [moved to chat](http://chat.stackexchange.com/rooms/54826/discussion-on-question-by-patel-simulating-from-this-density). – Glen_b Mar 05 '17 at 12:04
-
@Patel: what do you mean by "direct simulation"? Any valid method requires some steps that take computing time. An accept-reject algorithm may be faster than an inverse cdf approach, if this is what you mean. – Xi'an Mar 05 '17 at 13:59
1 Answers
[The cdf of this variable is $\Phi(x)-x\phi(x)$ but that's not likely to yield a convenient way to generate via the inverse-cdf method.]
Transformation is fairly easy -- if $X$ has the specified density, then $Y=\frac12 X^2$ has a simple, well-known distribution that is often available in statistical computing environments already (it is in R for example; it should also be available in many libraries)
If you're unfamiliar with transforming random variables, it's covered in detail in many places - see here for example, or here, and in this question CDF of transformed random variable; the calculations are straightforward substitution in a formula and one very simple differentiation. There's a detailed (and related) example discussed here.
So if you can generate from the appropriate distribution for $Y$, then $X=Z\sqrt{2Y}$ (where $Z$ is a random sign, ie. $\pm 1$ with equal probability) will have the distribution you're after.
(Actually the factor of $2$ could be incorporated in the original generation by changing the scale parameter, which may be slightly more convenient, avoiding the need to double $Y$ before taking the square root - because it would have been doubled at the previous stage)
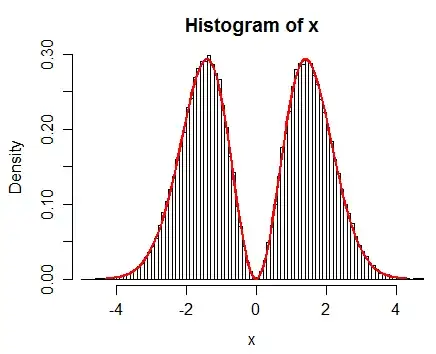
We can see that this method works; here's a histogram of a large sample generated using this approach, and the functional form of the density you specified drawn over the top:
While this is very convenient, if efficiency is an issue it's not likely to be faster than a well-chosen variant of the accept-reject method (ratio-of uniforms counts as one possible variant of accept-reject; it might be suitable particularly if accompanied by its own transformation -- in particular, one not requiring a square root, in the interests of speed)