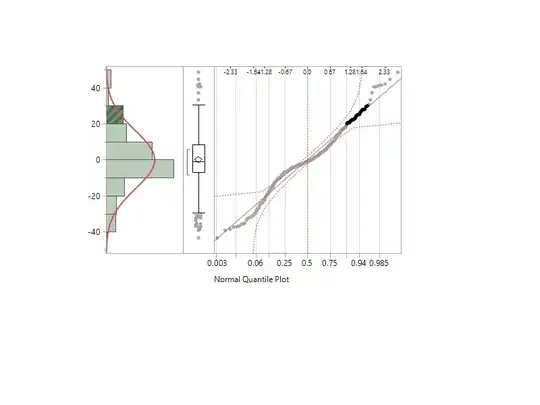
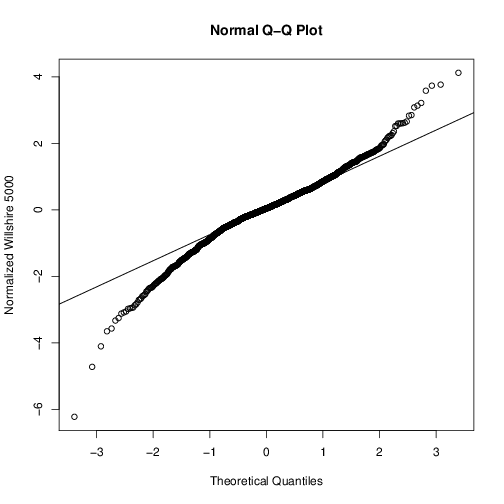
Growth rates must be distributed as some variation of the Cauchy distribution. I have written a series of papers on this. The Cauchy distribution has no mean so it has no variance or covariance. You can find my author page at https://papers.ssrn.com/sol3/cf_dev/AbsByAuth.cfm?per_id=1541471
Start with the paper titled "The distribution of returns," and then switch to the paper on Bayesian methods. Generally speaking, there is no admissible non-Bayesian solution though in specific cases there is a maximum likelihood solution that can be used if a null hypothesis method is required. The Bayesian likelihood function is always minimally sufficient.
You can communicate with me through the address on the author page. Because there is no variance or covariance, ANOVA and ANCOVA are impossible.
EDIT
With regard to the comments:
1)If I say it's Cauchy, and therefore rule out ANOVA and ANCOVA, what are my options?
Bayesian regression is still available. Your likelihood function would be $$\frac{1}{\pi}\frac{\sigma}{\sigma^2+(y-\beta_0-\beta_1x_1-b_2x_2\dots\beta_nx_n)^2}$$
The meaning is very different from OLS, though. OLS is from a convergent process, such as water going down a drain. This can be conceived as a double pendulum problem, and as such has limited predictive capapcity. For example, if you had $y|x$ you could think of $x$ as the upper pendulum and $y$ as the lower pendulum attached to the top pendulum. So, while $y$ is affected by the movement of $x$ it does not mean they are even moving in the same direction with a positive correlation. A pendulum swinging to the left could cause the other pendulum from momentum to swing to the right.
There is a tight linkage between the double pendulum problem, which is the first real observed problem in chaos theory, and regression in this case.
The proper interpretation is that, for example, if $y=1.1x$ then 50% of the time $y$ will be greater than $1.1x$ and fifty percent of the time it will be less than $1.1x$. You may be able to make stronger statements if there are other properties in your system, such as non-negativity.
2) I've read that Cauchy is problematic if residuals are almost normal.
This does not matter. You can find, or even construct, cases where the Cauchy distribution is indistinguishable from a normal distribution. Generally speaking there is no admissible non-Bayesian solution for most standard problems. This is a problem for someone trained only in Frequentist methods, but is not a problem per se. If a null hypothesis is required by the nature of the problem, then the only close solution would be quantile regression or Theil's regression. The problem with either is that, in the above equation, $x_1$ and $x_2$ are not independent, but they are also not correlated.
The question is not Gaussian versus Cauchy by some empirical test, but which should I have from theory. A certain percentage of the time, data drawn from a pure normal distribution will falsify a test of normality through chance alone. While it is sometimes true we do not know the likelihood function and must test for it, sometimes we do. This is a case where we do.
3) Is this really growth rate if I only have initial and final length?
Yes that is a growth rate, it is just a growth rate with limited observations per creature.
Not asked
Is there anything similar to anova or ancova? The answer is "it is unclear." If you will notice there is only one scale parameter in the likelihood and this does not depend on the number of variables. The scale parameter is a composite of the separate scale parameters, but it is not clear that there is any way to take advantage of this.