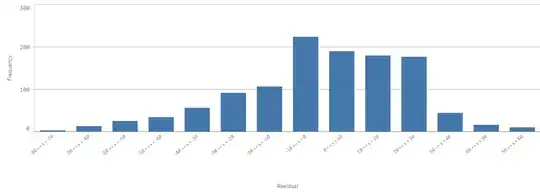
My data has 1700 rows and 7 features. I have built a linear regularized (Lasso) model (since I started with around 600 features which were highly correlated). After choosing the best model, I observe that there is drift trend in my residual plot.
Now this kind of trend violates normal error assumption of linear regression.
- We are overestimating the lower values and underestimating higher values. What steps can I take to handle this issue?
- Is it happening because of scarcity of data at both ends?
Please let me know if you need more information about the problem or data.