1

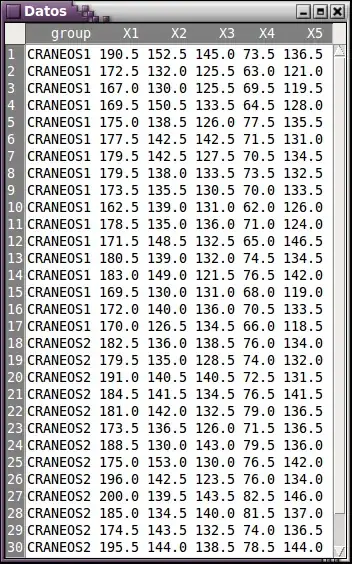
I hope you can help me with this question:

I have a time series data (25 years) that I will analyze to find temporal changes on seasonality over time. I am using linear regression and my model includes year (as a continuous variable) and the date in which the nest was initiated as explanatory variables. My response variable (eggs survival) was estimated as the proportion of eggs that survive in successful nests (meaning there was at least one egg in the nest at the end of the reproductive season) over the incubating period (# eggs counted at the end of incubation / #of eggs counted at the beginning of incubation). One of the years has a small sample size (n=35) compared to the rest (range without small sample size year goes from 69-338). Should I delete it from my dataset? What can I do?

If yes: I am using year as a continuous variable (year = 0 - 24), should I break the numbers (example: 0-7 and then continue 9-24) or should I number the years like if this year with small sample size doesn't exist?

UPDATE: This is the plot residuals vs fitted values, according to AIC my best model shows changes over time (the interaction is significant), however the r2 is 0.02. Any advice?

enter image description here

UPDATE2:

I applied robust linear regression with an exponential transformation, weights as variance/n and deleted an outlier. This is the best I could fit the data. Can you please give me your opinion?: 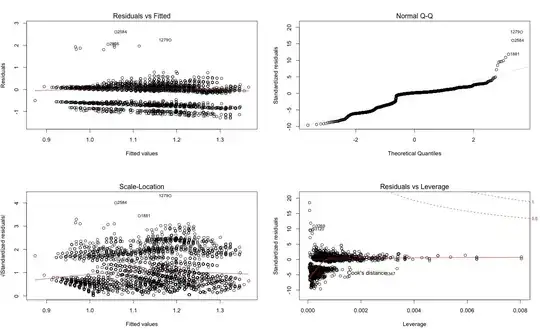enter image description here

though, the robust regression makes not much difference. Using simple linear regression with weights and exponential transformation (because I have positive and negative values, log is not possible) my r2 improves a bit to 0.04

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
MSS
  • 267
  • 2
  • 9
  • What is the context, can you tell us? We need context for this to be answerable. There are many possibilities, like using a weighted analysis. You should probably not delete the data point, deleting correct data is seldom good! But tell us the details ... – kjetil b halvorsen Feb 10 '17 at 19:05
  • 1
    You haven't yet given us some critical information, such as what--if anything--you intend to do with this time series. If you plan to model it then you will want to retain both counts in each year, because replacing them by a proportion wipes out important information. You will not want to remove data just because one count was small: that biases the data and incidentally makes many standard time-series analysis methods inapplicable or more difficult to use. – whuber Feb 10 '17 at 19:21
  • Done! thank you for your comment. I hope my question is complete now. – MSS Feb 10 '17 at 19:39
  • 1
    It's looking better, thank you. Did you really intend to write "temporal changes on seasonality" or "temporal changes *and* seasonality"? If it's the former, what do you mean by that? And what do you mean by seasonality with yearly variables? – whuber Feb 10 '17 at 20:11
  • yes, the first one. This data comes from a seasonal environment (there is a normal decrease in food resources every year), but there are also changes in the ecosystem because of climate warming, so we want to know if there are changes on this seasonal pattern over 25 years. – MSS Feb 10 '17 at 20:54
  • How do you have any information about this seasonal environment when you only have annual data? Or are your data obtained more frequently then annually? – whuber Feb 10 '17 at 21:59
  • 1
    it is a migratory species, it breeds only in the summer, once they have their chicks they go back to the south. So the period of time when we collected data is similar every year. Then the monitoring (and therefore my dataset) consists of data collected every summer, about 20 days (nest initiation in my model) over 25 years.We know the environment is changing because we have done studies about climate and other species, but in this analysis we only want to know the trends for this species. – MSS Feb 10 '17 at 23:09
  • What is your reasoning about nesting "efficiency" ? You said that your continuous explanatory variable is year number. That means that your hypothesis is that the higher is year number the higher (or lower) is nesting efficiency. But why ??? With all my little knowledge about birds,I think the birds don't really care what is the year number and therefore your zero R2 does not surprise me at all. Even including the day number in the model makes no sense to me (again -the birds don't care about the date at all). So I think its perfectly reasonably that your model has zero R2. – Branislav Cuchran Feb 13 '17 at 22:43
  • Hi @King'sSolomonHorse, we are looking for changes in the nesting season over time. The fact that birds do not care about the day is actually the problem we study, because the environment is changing but the birds are not (because they come from ecosystems in the south with different environmental change). So we want to see if this is affecting them and how this trends are. thank you! – MSS Feb 13 '17 at 22:52

1 Answers1

0

No, you should not remove the data point at first. Regress the data and look at the results. The summary results will tell you if you have enough data, using something like adj-R2. If the results of the regression are not significant, then you may think about removing it. It is more important that the total number of data points is large enough.

One bad year of data will have little to no effect on a long range effect. You are trying to demonstrate a linear relationship over 25 years, so one year of low observations will not have a large effect on the total regression. Also, years in the middle will have less effect on the regression's slope.

Can you run the regression and post the results?

Your regression line should look something like this: discrete regression example

Maddenker
  • 361
  • 3
  • 11
  • 1
    These are good general recommendations for regression. The present situation presents two important complications, however. First is that the data deserve different weights (or modeling with a suitable GLM) because the variance of the response changes (a lot) with the number of nests each year. Second is that this time series likely exhibits important levels of serial correlation. A good answer needs to exhibit an awareness of these complications and suggest approaches to cope with them. – whuber Feb 11 '17 at 18:38
  • Only the data can tell you that there is serial correlation. Not you. Not me. MSS needs to perform some analysis and interpret the results. – Maddenker Feb 13 '17 at 01:24
  • Serial correlation? is it enough if I weight my values? Can you give me an advice about how to do the weights? thanks a lot! – MSS Feb 13 '17 at 04:18
  • 1
    What you write in your comment is true--but your answer stands in opposition to it. It's difficult to see how your recommendations could be defended without making some strong assumptions. If you truly believe additional analysis and interpretation are needed--which is reasonable--then your answer would be more helpful by pointing that out rather than making assertions that very might be false or recommendations that might be counterproductive. – whuber Feb 13 '17 at 14:22
  • In my case, can I use weights like suggested here http://stats.stackexchange.com/questions/51378/weighting-the-response-variable-in-an-lm?noredirect=1&lq=1 as variance/n (so each observation will have the weight of that year? – MSS Feb 13 '17 at 20:54