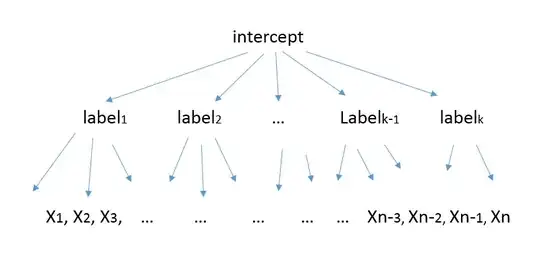
According to e.g. https://stats.stackexchange.com/a/61466/14346, the following simple model: $$ x_{label} = a_{label} + e_{label} $$ writes in lmer syntax as:
x~1|label
However, I do not manage to understand this formulation : What is the meaning of this when dealing with multiple observations i.e. multiple (and different) observations $x_{label}$ for a given label ?