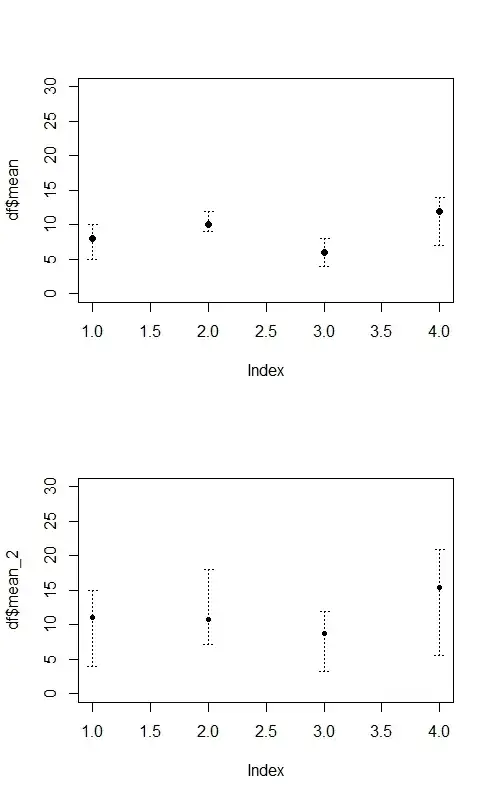
I've fitted a binomial GLM, which returns the summary table shown below. What could be the reason that the estimated value of the predictor spikeCountj2m4 has such a large standard error, compared to the other predictors? (highlighted by a red circle in the table below).
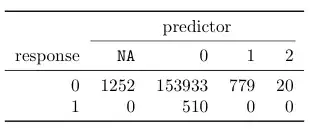
See also the contingency table of the response spikeCountj1 and the predictor spikeCountj2m4 below. Is it possible that the standard error in question is inflated because there are no observations where the predictor is different than zero when the response is equal to one? If so, how can I remedy this?