1

I have dataset of numbers given as

$Y = x $ if $ x >= 5 $ and $x<=9$

and $x$~$N(\mu,\sigma^{2})$. Or we can say that we have the data-set as subset of normally distributed data-set.

Now for the given data(histogram given below), how do i estimate those unknown parameters $\mu$ and $\sigma^{2}$ using MLE in R?

enter image description here

Sanjeev
  • 87
  • 9

1 Answers1

4

The truncated density is the normal distribution but multiplied with 1/(F(right)-F(left)) so that its integral is 1. So one idea would be to use this truncated density for the calculation of the loglikelihood.

For example, in R:

ll1 <- function(param, dat, left, right) {
    mu <- param[[1]]
    sigma <- param[[2]]
    -sum(dnorm(dat, mean=mu, sd=sigma, log = TRUE)-log(pnorm(right, mean=mu, sd=sigma)-pnorm(left, mean=mu, sd=sigma)))
}

set.seed(1)
x <- rnorm(1000, mean=6, sd=1.2)
y <- x[x>=5 & x <= 9]
optim(par=c(mean(y), sd(y)), fn=ll1, dat=y, left=5, right=9)[["par"]]
# [1] 5.960276 1.280664

However, after getting downvoted I am not sure if that is the right thing to do. Looking at the chart of the loglikelihood (the red dot represents the true parameters we happen to know), something seems wrong:

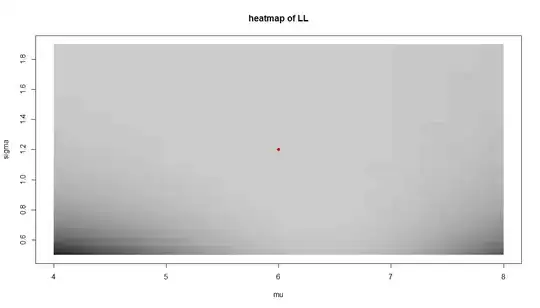
heatmap of loglikelihood

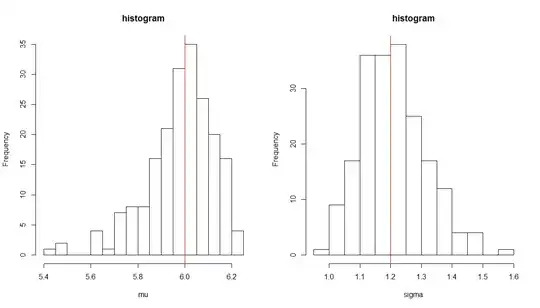
It looks to me as if the loglikelihood does not have a minimum at the true parameter. On the other hand, repeating the fitting again and again with different input data, yields histograms that look good:

histogram of the fitted parameters (200 repetitions)

Karsten W.
  • 667
  • 6
  • 25
  • What exactly is this code doing? – Matthew Drury Feb 02 '17 at 18:53
  • Well, I tried to calculate the density of the truncated distribution, ... – Karsten W. Feb 02 '17 at 19:06
  • 1
    Unless I'm mistaken, this code is doing the right thing. To be a proper answer though, you will need to describe *why* it is the right thing to do. – Cliff AB Feb 02 '17 at 19:44
  • Right, it was my downvote, I'll remove it since my point was made. Sorry, I should have been more clear in my comment. I think it will be a good answer with a full description of the algorithm. – Matthew Drury Feb 02 '17 at 20:52
  • Thanks for solution. Could you please help me selecting type of optimization method for optim R function i.e when to use which optimization? – Sanjeev Feb 04 '17 at 12:38
  • Since this is a convex optimization problem, the default Nelder-Mead should work just fine. If time is a factor, you could provide a gradient function and change to conjugate gradient method ("CG"), which should be faster. – Karsten W. Feb 09 '17 at 18:45