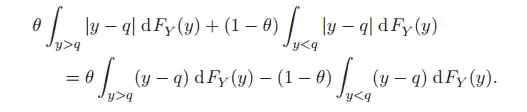The integral is used to define the (population) quantile of the random variable $Y$, while the summation is for the linear quantile regression, which aims at estimating the regression quantile coefficients $\beta_q$ using data $(y_i,x_i),i=1,\ldots,N$. Both employ the quantile check loss $\rho_{\theta}(u)=u(\theta-I(u<0))$. Indeed, the integral can be viewed as $E[\rho_{\theta}(Y-q)]$ and the summation is $\sum_{i=1}^N\rho_{\theta}(y_i-x_i'\beta_q)$. An analogy is the definition of the expectation vs. that of the least squares estimation. Specifically, $E(Y)$ can be viewed as the minimizer of the integral $\int_{-\infty}^{\infty}(y-m)^2\mathrm{d}F_Y(y)$ and the least squares estimator (of the coefficient vector) is obtained by minimizing $\sum_{i=1}^N(y_i-x_i'\beta_m)^2$.