How to benchmark an ACD model?

Question

I have trained an Autoregressive Conditional Duration (ACD) model on some transactions data. Then, I test it against some other transactions data to check how well it predicts the time interval between two trades. Optically, the results seem OK (cf. Figure). 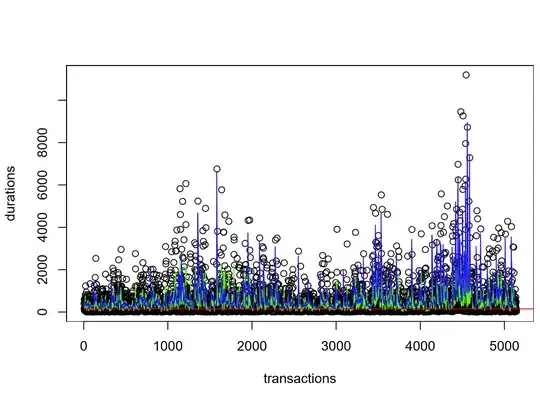In blue, the ACD predictions; In green, the values of moving average using the last 5 durations; In red, the value of the median in-sample.

If I report the errors as "the median (or the mean, or a different quantile) of the absolute errors between the real value and the predicted value", then I obtain that the in-sample median is the best model though it doesn't capture the dynamics at all!

What would be a 'fair' way to benchmark this model?

Answer 1

I'm not surprised at the median performing "best" in terms of the absolute error. If there are truly no dynamics and all observations are iid, then the median will minimize the expected absolute error (Hanley et al., 2001, The American Statistician). And it's not uncommon for the mean or other simple methods to outperform more complex models.

The dynamics may not quite so clear-cut, or at least the signal may not be strong and predictable enough that modeling them improves on the simple median.

You may need to revisit your loss function. Maybe the absolute error does not represent your loss accurately.