I am trying to prove or disprove that the difference between Spearman's Correlation and Kendall's Correlation is no more than 1 (or less, the tighter the merrier).
I am assuming there are no ties.
In an attempt to disprove the result using a counter example, I checked all possibilities for vectors with length 8. Got some pretty pictures but no counter example:
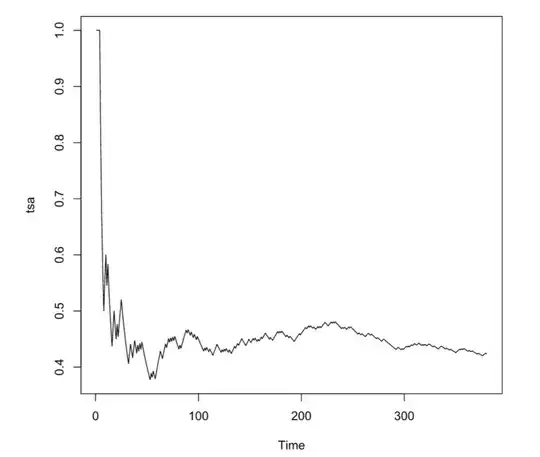
difference:
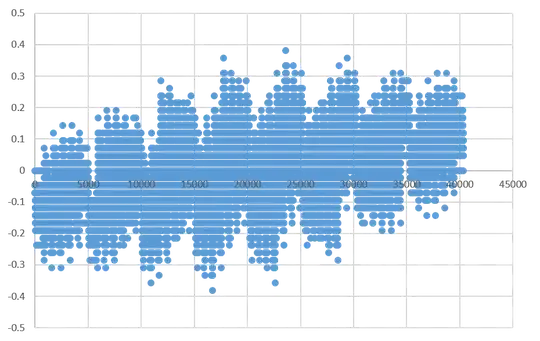
The difference is never more than 0.4 in this case, so I think it is true, but I was unable to prove it.