5

What is the linear algebraic and geometric interpretation of the sentence found on this post:

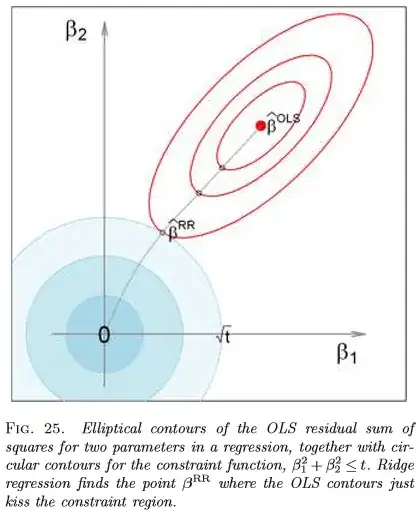
When $y = X\beta + e$, the least squares problem which imposes a spherical restriction $\delta$ on the value of $\beta$, [which] can be written as

\begin{equation} \begin{array} &\operatorname{min}\ \| y - X\beta \|^2_2 \\ \operatorname{s.t.}\ \ \|\beta\|^2_2 \le \delta^2 \end{array} \end{equation}

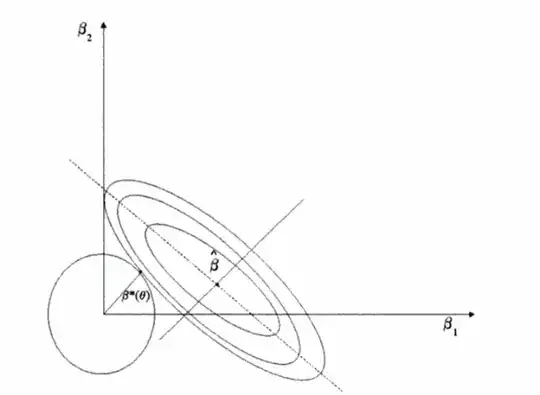
It sounds as though it has to be connected with the concept of spherical errors, but there is likely more to it. Further I was intrigued by this illustration comparing OLS to ridge regression:

enter image description here

Source: A First Course in Linear Model Theory / Edition 1 by Nalini Ravishanker, Dipak K. Dey, Dipak K. Dey

with the text:

We can characterize ridge regression as a restricted least squares problem. Consider the least squares in the centered and scaled multiple regression model $\bf y^*=X^*\beta^*+\varepsilon$ subject to the spherical restriction $$\beta^{*'}\beta^*\leq d^2$$ for a given value $d^2.$

Continuing along the hints given by W. Huber in the comments, I wonder if this is related to the ellipsoid representation, and the geometric interpretation of ridge regression as a contained OLS optimized at the locus of osculation determined by $\mathbf \beta^\top K \beta$:

enter image description here

Source: Elliptical Insights: Understanding Statistical Methods through Elliptical Geometry Statistical Science 28(1) · February 2013, Michael Friendly and Georges Monette

Community
  • 1
Antoni Parellada
  • 23,430
  • 15
  • 100
  • 197
  • 3
    For $\beta\in\mathbb{R}^k$, the equation $||\beta||^2\le\delta^2$ is satisfied by the points in the ball (aka "sphere") of radius $\delta$ centered at the origin of $\mathbb{R}^k$. I believe that's all that the phrase "spherical restriction" was intended to mean. – whuber Jan 18 '17 at 16:51
  • @whuber Even centered, though, each $ \beta_i$ coefficient is different. Do you draw this hypersphere with a radius equal to the smallest coefficient? And is it just a statement implying that the coefficients are all less than infinity? I am still not seeing it... – Antoni Parellada Jan 18 '17 at 16:56
  • You seem to be confusing a ball with a line. The constraints require only that $\beta$ lie within the ball, not that it lie on the line $\beta_1=\beta_2=\cdots=\beta_k$! Note that both $\delta$ and $d$ are "given values": that is, they are not free to vary, but are specified as part of the problem. – whuber Jan 18 '17 at 16:58
  • @whuber I see the picture now - not on the surface of the sphere, but within. Where are the values of $\delta$ specified? – Antoni Parellada Jan 18 '17 at 16:59
  • In Ridge Regression, you don't know $\delta$, so you solve this optimization problem for a wide range of values of $\delta$ and you explore how the solutions vary with $\delta$. See http://stats.stackexchange.com/questions/154706 for an example. (Usually the columns of $X$ are first standardized. The coefficient estimates are graphed against $\delta$ in a "ridge trace" plot.) – whuber Jan 18 '17 at 17:02
  • @whuber Oh, I see it now... but I thought that we were still within OLS... That ridge regression with the elliptical form was the next step, but that $\delta$ had already surfaced as a concept *before* moving from OLS to ridge. – Antoni Parellada Jan 18 '17 at 17:05
  • 1
    After Ridge Regression was invented, it was re-interpreted as the solution to OLS with a particular kind of Bayes prior on $\beta$. Within that interpretation, $\delta$ does have some meaning (related to how small you think the coefficients ought to be). – whuber Jan 18 '17 at 17:07
  • @whuber Magisterial! As always! From your comments, I gather that, although you pre-empted the answer, it's still worthwhile to keep the OP open. Let me know if you disagree. – Antoni Parellada Jan 18 '17 at 17:08
  • I did not intend to pre-empt any answers: after all, none of these comments have actually addressed your question, which appears to concern possible connections to spherical errors. I was only trying to clarify the meaning of "spherical restriction" (which does not appear to be a commonly used term in statistics). – whuber Jan 18 '17 at 17:13
  • @whuber Very good. Thank you very much! You have solved my main hurdle in understanding this. – Antoni Parellada Jan 18 '17 at 17:15

1 Answers1

2

As explained in the comments, the problem is ridge regression, where the squared error is minimized subject to a bound on the $\ell_2$ norm of $\beta$.

As far as I can discern, constraining the $\ell_2$ norm of $\beta$ is not connected to linear model assumptions that the error is spherical. After all, using Bayesian language, the likelihood $\pi(y|\beta)$ being spherical does not suggest that the prior $\pi(\beta)$ should be too.

user795305
  • 2,692
  • 1
  • 20
  • 40