3

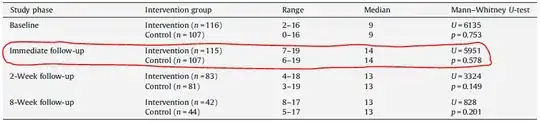
I'm conducting a meta-analysis and one of the studies only reports Mann-Whitney $U$ statistic. The table with results is pasted below.

enter image description here

Circled in red is the $U$ statistic that tests the differences between intervention and control group in post-intervention settings.

I wonder how to derive appropriate effect size (note that for other studies I use Hedges' $g$) and associated standard error from presented data.

My initial attempt goes as follows. Because we have large samples ($n > 20$) the $U$ approaches a normal distribution and the null hypothesis could be tested by a $Z$-test. So I compute $Z$ using the formula

$$ Z = \frac{U - ((n_c \times n_i) / 2)}{SD}, $$ where $SD$ is computed by $$ SD = \sqrt{\frac{(n_c \times n_i) \times (n_c + n_i + 1)}{12}}. $$

This yields $Z = -0.42$. Referring to the previous post, the effect size could be computed as $$ r = \frac{Z}{\sqrt{n_c + n_i}} = \frac{-0.42}{\sqrt{107 + 115}} = -0.02. $$

My questions are:

  • Could I use derived $r$ as an estimate for Hedges' $g$
  • How should I compute standard error?
Community
  • 1
Andrej
  • 2,131
  • 2
  • 18
  • 26
  • 3
    What do you want the standard error of? Since $U$ depends only on the ranks, *it tells you absolutely nothing about the actual values*. There's no way you can compare it to Hedges' $g$. – whuber Jan 14 '17 at 21:48

1 Answers1

1

You have two not very satisfactory options here.

You could say "Suppose they had done a $t$-test and got exactly that $p$-value, what value of Hedges' $g$ would that have corresponded to?". Whether you can persuade your audience that this is not a step too far is another matter.

You could revert to a meta-analysis of $p$-values which would give you an overall $p$-value but would not give you an overall effect size. There are a number of methods for this and there is a tag here.

But, as I say, neither of these is completely satisfactory.

mdewey
  • 16,541
  • 22
  • 30
  • 57