Background
Suppose I have observations $y=\{x_1,x_2,...,x_n\}$ of a binary variable $x_i\in\{0,1\}$ (assumed to be IID). Observations are generated by some complicated and unknown system $\mathcal F$. To simulate/predict the output of the system I use a function $f(θ)$, parameterized by model parameters $\theta$, leading to model predictions $\hat y_i(\theta)$. My aim is to learn something about the underlying system by interpreting the model parameters $\theta$, i.e. the overall goal is to infer the posterior distribution over $\theta$.
Likelihood function
I have considered two different likelihood functions to represent the observations:
Representation 1 - Bernoulli distributions. Represent observations by modeling the sequence of observations by
$$\begin{eqnarray}\displaystyle p(y|\gamma,\theta)=\prod_{i=1}^n\gamma^{I(y_i=\hat y_i(\theta))}(1-\gamma)^{I(y_i\neq\hat y_i(\theta))} = \gamma^{s(\theta)}(1-\gamma)^{n-s(\theta)}\end{eqnarray}, \qquad (1)$$
with $\gamma$ being the probability of succes, i.e. correspondence between model prediction and observation, $I()$ being the indicatior function that returns 1 if argument is true and 0 otherwise, and $\displaystyle s=\sum_i I(y_i=\hat y_i(\theta))$.
Representation 2 - Binomial distribution. Represent data by modeling the number of successes
$$\begin{eqnarray}\displaystyle p(y|\gamma,\theta)=\frac{n!}{s(\theta)!(n-s(\theta))!}\gamma^{s(\theta)}(1-\gamma)^{n-s(\theta)}\end{eqnarray}. \qquad (2)$$
Prior
Beta prior
$$\begin{eqnarray}p(\gamma|\alpha,\beta)=\frac{1}{B(\alpha,\beta)}\gamma^{\alpha - 1}(1-\gamma)^{\beta - 1}\end{eqnarray} $$
Marginalize over "success probability"
I am primarily interested in inferences regarding the parameter vector $\theta$ and not $\gamma$. Therefore I marginalize over the success probability $\gamma$
$$\begin{eqnarray}p(y|\theta)=\int_0^1p(y|\gamma,\theta)p(\gamma|\alpha,\beta) d\gamma\end{eqnarray},$$
where I assume $\gamma$ and $\theta$ being independent.
Using "likelihood representation 1" above I get
$$\begin{eqnarray} \displaystyle p(y|\theta)&=&
\int_0^1 \gamma^{s(\theta)}(1-\gamma)^{n-s(\theta)}\frac{1}{B(\alpha,\beta)}\gamma^{\alpha - 1}(1-\gamma)^{\beta - 1} d\gamma \\
&=&\frac{1}{B(\alpha,\beta)}\int_0^1 \gamma^{s(\theta)+\alpha-1}(1-\gamma)^{n-s(\theta)+\beta-1} d\gamma \\
&=&
\frac{B(s(\theta)+\alpha,n-s(\theta)+\beta)}{B(\alpha,\beta)}.\qquad (3)
\end{eqnarray} $$
Using "likelihood representation 2" above I get
$$\begin{eqnarray} \displaystyle p(y|\theta)&=&
\int_0^1 \frac{n!}{s(\theta)!(n-s(\theta))!}\gamma^{s(\theta)}(1-\gamma)^{n-s(\theta)}\frac{1}{B(\alpha,\beta)}\gamma^{\alpha - 1}(1-\gamma)^{\beta - 1} d\gamma \\
&=&\frac{n!}{s(\theta)!(n-s(\theta))!B(\alpha,\beta)}\int_0^1 \gamma^{s(\theta)+\alpha-1}(1-\gamma)^{n-s(\theta)+\beta-1} d\gamma \\
&=&
\frac{n!B(s(\theta)+\alpha,n-s(\theta)+\beta)}{s(\theta)!(n-s(\theta))!B(\alpha,\beta)}.\qquad (4)
\end{eqnarray} $$
Below, I plot eq. (3) in (A) and eq. (4) in (B) and their logarithms in (C) and (D), respectively, for an example with $n=10$ observations
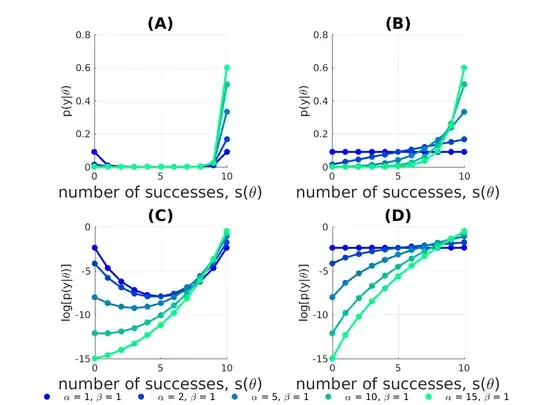
The two likelihood representations in eq. (1-2) lead to quite different behavior in $p(y|\theta)$. For example, using a uniform prior ($\alpha =1, \beta = 1$), $p(y|\theta)$ is uniform (plot (B,D)) when using likelihood representation 2 eq. (2) , whereas likelihood representation 1 eq. (1) concentrates most of the probability mass of $p(y|\theta)$ near low and high values of $s(\theta)$ (plot (A,C)).
If I trust my model and believe that it should perform better than chance, I can incorporate this assumption into the probabilistic model by changing the hyperparameters governing the prior over $\gamma$. Fixing $\beta=1$ and letting $\alpha>1$ we see, that likelihood representation 2 eq. (2) results in $p(y|\theta)$ being monotonically increasing as a function of successes $s(\theta)$ plot (B,D). When using likelihood representation 1 eq. (1) this also biases the probability mass towards large values of $s(\theta)$, however, $\alpha\geq n+\beta$ before $p(y|\theta)$ is increasing monotonically as a function of successes $s(\theta)$.
Questions
1) Theoretical: From a theoretical point of view, are there any reasons for preferring either likelihood representation 1 eq. (1) or likelihood representation 2 eq. (2)?
2) Practical: The above probabilistic model is part of a larger probabilistic setup, where I also model the prior governing $\theta$ as well as model other types of observations. For inferences over $\theta$ I use MCMC. Using such an iterative procedure, one concern with using likelihood representation 1 eq. (1) could be, that the sampling procedure get trapped in regions with low $s(\theta)$ because of non-monotonic behavior of $p(y|\theta)$ if $\alpha<n+\beta$ (imagine $p(y|\theta)$ being sharply peaked at low and high success probabilities). Of course I could assign a high value to $\alpha$, but this, in turn, condenses much of the probability mass near maximal values of $s(\theta)$ relative to the case when using likelihood representation 2 (compare A vs. B). Would this concern vote in favor of using likelihood representation 2?