23

Consider the elementary identity of variance:

$$ \begin{eqnarray} Var(X) &=& E[(X - E[X])^2]\\ &=& ...\\ &=& E[X^2] - (E[X])^2 \end{eqnarray} $$

It is a simple algebraic manipulation of the definition of a central moment into non-central moments.

It allows convenient manipulation of $Var(X)$ in other contexts. It also allows calculation of variance via a single pass over data rather than two passes, first to calculate the mean, and then to calculate the variance.

But what does it mean? To me there's no immediate geometric intuition that relates spread about the mean to spread about 0. As $X$ is a set on a single dimension, how do you view the spread around a mean as the difference between spread around the origin and the square of the mean?

Are there any good linear algebra interpretations or physical interpretations or other that would give insight into this identity?

Mitch
  • 1,691
  • 2
  • 18
  • 33
  • 7
    Hint: this is the [Pythagorean Theorem.](http://stats.stackexchange.com/search?q=pythagorean+variance) – whuber Jan 03 '17 at 18:48
  • I would definitely write the second term as $(EX)^2$. My brain reads $E^2 X$ as "apply the $E$ operator twice". – Matthew Drury Jan 03 '17 at 18:49
  • 1
    @Matthew I wonder what "$E$" is intended to mean. I suspect it is *not* an expectation, but just shorthand for the arithmetic mean. Otherwise the equations would be incorrect (and nearly meaningless, since they would then equate random variables with numbers). – whuber Jan 03 '17 at 19:00
  • I agree with Bill Huber the use of summation in the first line confuses the expectation of a random variable with a sample estimate of expectation. But if you throw out the right hand side of the first line it really could be an expectation in the sense that Bill Huber means. – Michael R. Chernick Jan 03 '17 at 19:16
  • The edit makes this look much better. – Michael R. Chernick Jan 03 '17 at 19:17
  • To me the simple algebraic proof is satisfactory. I am curious as to why you seek a geometric demonstration or anything else? – Michael R. Chernick Jan 03 '17 at 19:19
  • 2
    @whuber Since inner products introduce the idea of distances and angles, and the [inner product of the vector space of real-valued random variables](http://www.math.uah.edu/stat/expect/Spaces.html) is defined as $\mathbb E[XY]$ (?), I wonder if some geometrical intuition could be given via the triangle inequality. I have no idea how to proceed, but I was wondering if it makes any sense. – Antoni Parellada Jan 03 '17 at 19:21
  • 1
    @Antoni The triangle inequality is too general. An inner product is a much more special object. Fortunately, the appropriate geometrical intuition is precisely that of Euclidean geometry. Moreover, even in the case of random variables $X$ and $Y$, the necessary geometry can be confined to the two-dimensional real vector space generated by $X$ and $Y$: that is, to the Euclidean plane itself. In the present instance $X$ does not appear to be an RV: it's just an $n$-vector. Here, the space spanned by $X$ and $(1,1,\ldots, 1)$ is the Euclidean plane in which all the geometry happens. – whuber Jan 03 '17 at 19:52
  • I here a lot lately about all this geometry of random variables which many years ago I learned about from Brad Efron in my first Math Stat graduate class at Stanford. Efron published on the geometry of exponential families. But I haven't heard the term Hilbert space mentioned. Doesn't this rest on random variables being functions defined on a Hilbert space? – Michael R. Chernick Jan 03 '17 at 19:56
  • @lam Thanks for the parens edit. I personally can't stand the unadorned $EX^2$ vs $E^2X$ thing because I trip over it all the time. But I see it all the time in textbooks. Thank you for editing. – Mitch Jan 03 '17 at 20:07
  • @whuber I don't see the pythagorean connection. Can you be more explicit? What are the two coordinates? Here there is no Y (that I can tell) – Mitch Jan 03 '17 at 20:10
  • @Mitch no problem.. i couldn't help it either :).. if i think of some other interpretation, i will add it to the answer below later.. up to date, that's how i visualize the definition of variance.. – Starz Jan 03 '17 at 20:19
  • 1
    @Michael The Hilbert space formulation is rarely needed. As I pointed out here (and in many related answers), the geometry typically occurs within finite-dimensional subspaces, almost always of two or fewer dimensions. Mitch, the coordinates consist of a multiple of $X$ and another multiple of $Y=(1,1,\ldots, 1)$, which can be written as the linear combination $xX+yY$. A value of $y$ is chosen so that $yY$ (whose length you write "$E(X)$") and $X-yY$ (whose squared length is the variance) are perpendicular: they form the legs of a right triangle whose hypotenuse is $X$ itself. – whuber Jan 03 '17 at 20:26
  • 1
    There's a picture along with an algebraic demonstration at http://stats.stackexchange.com/a/97881/919. That thread concerns least-squares regression, but the present question is the simplest possible instance of that, where there is a constant term (with parameter $\beta_0$) and no other terms. – whuber Jan 03 '17 at 20:41
  • @whuber Thanks for answering the question in my comment. – Michael R. Chernick Jan 03 '17 at 20:50
  • @whuber That all looks great and it seems relevant, but I'm having a hard time seeing what's what for variance as the simplest example. Would you mind reworking that for just variance? A lot of the leaps from line to line aren't entirely obvious (eg 'obviously perpendicular' not to me because I;m never sure what the direction of reasoning is) – Mitch Jan 03 '17 at 21:36
  • 1
    @MichaelChernick re "To me the simple algebraic proof is satisfactory. I am curious as to why you seek a geometric demonstration or anything else?" It helps to understand 'why'/allows easier thought/generalization/allows more accurate informal explanations. – Mitch Jan 03 '17 at 21:41
  • 3
    Setting $\hat\beta_1=0$ in the reply I linked to, and dividing all terms by $n$ (if you wish) will give you the full algebraic solution for the variance: there's no reason to copy it all over again. That's because $\hat\beta_0$ is the arithmetic mean of $y$, whence $||y-\hat y||^2$ is just $n$ times the variance as you have defined it here, $||\hat y||^2$ is $n$ times the squared arithmetic mean, and $||y||^2$ is $n$ times the arithmetic mean of the squared values. – whuber Jan 03 '17 at 22:04

5 Answers5

23

Expanding on @whuber's point in the comments, if $Y$ and $Z$ are orthogonal, you have the Pythagorean Theorem:

$$ \|Y\|^2 + \|Z\|^2 = \|Y + Z\|^2 $$

Observe that $\langle Y, Z \rangle \equiv \mathrm{E}[YZ]$ is a valid inner product and that $\|Y\| = \sqrt{\mathrm{E}[Y^2]}$ is the norm induced by that inner product.

Let $X$ be some random variable. Let $Y = \mathrm{E}[X]$, Let $Z = X - \mathrm{E}[X]$. If $Y$ and $Z$ are orthogonal:

\begin{align*} & \|Y\|^2 + \|Z\|^2 = \|Y + Z\|^2 \\ \Leftrightarrow \quad&\mathrm{E}[\mathrm{E}[X]^2] + \mathrm{E}[(X - \mathrm{E}[X])^2] = \mathrm{E}[X^2] \\ \Leftrightarrow \quad & \mathrm{E[X]}^2 + \mathrm{Var}[X]= \mathrm{E}[X^2] \end{align*}

And it's easy to show that $Y = \mathrm{E}[X]$ and $Z = X - \mathrm{E}[X]$ are orthogonal under this inner product:

$$\langle Y, Z \rangle = \mathrm{E}[\mathrm{E}[X]\left(X - \mathrm{E}[X] \right)] = \mathrm{E}[X]^2 - \mathrm{E}[X]^2 = 0$$

One of the legs of the triangle is $X - \mathrm{E}[X]$, the other leg is $\mathrm{E}[X]$, and the hypotenuse is $X$. And the Pythagorean theorem can be applied because a demeaned random variable is orthogonal to its mean.

Technical remark:

$Y$ in this example really should be the vector $Y = \mathrm{E}[X] \mathbf{1}$, that is, the scalar $\mathrm{E}[X]$ times the constant vector $\mathbf{1}$ (e.g. $\mathbf{1} = [1, 1, 1, \ldots, 1]'$ in the discrete, finite outcome case). $Y$ is the vector projection of $X$ onto the constant vector $\mathbf{1}$.

Simple Example

Consider the case where $X$ is a Bernoulli random variable where $p = .2$. We have:

$$ X = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \quad P = \begin{bmatrix} .2 \\ .8 \end{bmatrix} \quad \mathrm{E}[X] = \sum_i P_iX_i = .2 $$

$$ Y = \mathrm{E}[X]\mathbf{1} = \begin{bmatrix} .2 \\ .2 \end{bmatrix} \quad Z = X - \mathrm{E}[X] = \begin{bmatrix} .8 \\ -.2 \end{bmatrix} $$

And the picture is: enter image description here

The squared magnitude of the red vector is the variance of $X$, the squared magnitude of the blue vector is $\mathrm{E}[X]^2$, and the squared magnitude of the yellow vector is $\mathrm{E}[X^2]$.

REMEMBER though that these magnitudes, the orthogonality etc... aren't with respect to the usual dot product $\sum_i Y_iZ_i$ but the inner product $\sum_i P_iY_iZ_i$. The magnitude of the yellow vector isn't 1, it is .2.

The red vector $Y = \mathrm{E}[X]$ and the blue vector $Z = X - \mathrm{E}[X]$ are perpendicular under the inner product $\sum_i P_i Y_i Z_i$ but they aren't perpendicular in the intro, high school geometry sense. Remember we're not using the usual dot product $\sum_i Y_i Z_i$ as the inner product!

Matthew Gunn
  • 20,541
  • 1
  • 47
  • 85
  • That is really good! – Antoni Parellada Jan 05 '17 at 01:28
  • 1
    Good answer (+1), but it lacks a figure, and also might be a bit confusing for OP because your Z is their X... – amoeba Jan 05 '17 at 13:01
  • @MatthewGunn, great answer. you can check my answer below for a representation where orthogonality is in the Euclidean sense. – jkt Jan 05 '17 at 20:14
  • I hate to be obtuse, but I'm having trouble keeping $Z$, $Var(X)$, and the direction of the logic straight ('because' comes at places that don't make sense to me). It feels like a lot of (well substantiated) facts are stated randomly. What space is the inner product in? Why __1__? – Mitch Jan 08 '17 at 17:10
  • @Mitch The logical order is: (1) Observe that a probability space defines a vector space; we can treat random variables as vectors. (2) Define the inner product of random variables $Y$ and $Z$ as $E[YZ]$. In an inner product space, vectors $Y$ and $Z$ are defined as orthogonal if their inner product is zero. (3a) Let $X$ be some random variable. (3b) Let $Y = E[X]$ and $Z = X - E[X]$. (4) Observe that $Y$ and $Z$ defined this way are orthogonal. (5) Since $Y$ and $Z$ are orthogonal, the pythagorean theorem applies (6) By simple algebra, the Pythagorean theorem is equivalent to the identity. – Matthew Gunn Jan 08 '17 at 18:10
  • a) "treat a random variable as a vector" - don't you mean a sample as a vector in a (suitable) inner vector space? b) is the inner product space really necessary? I think it obfuscates things (not particularly intuitive), just vectors and dot product are sufficient machinery c) Can you edit to summarize that var(X) is one leg and EX is another leg and $E[X^2]$ is the hypotenuse or the area on the hypotenuse or whatever. – Mitch Jan 08 '17 at 18:21
  • @Mitch A real valued random variable is a function from a sample space $\Omega$ to the set of real numbers $\mathbb{R}$. Imagine I have a random variable $X$ which takes the value of 235 if I flip heads and the value of 12 if I flip tails. The sample space $\Omega = \{H, T\}$. $X$ here is a function from $\Omega$ to $\mathbb{R}$, but you can conceptually think of it as the vector $\begin{bmatrix} 235 \\ 12 \end{bmatrix}$. Once you make this conceptual leap that random variables are vectors, you can talk about *orthogonal* random variables in the same way you talk about orthogonal vectors. – Matthew Gunn Jan 08 '17 at 18:29
  • @Mitch If you haven't taken a math class covering [linear algebra](https://en.wikipedia.org/wiki/Linear_algebra) yet, what I wrote down may look a bit abstract. At the end of the day, I'm basically going through the exact same algebra you would do to prove the identity but adding the interpretation that $E[X]$ and $X - E[X]$ are orthogonal, and that makes the identity equivalent to pythaogrean theorem. – Matthew Gunn Jan 08 '17 at 18:43
  • @MatthewGunn As I mentioned, all the algebra works perfectly fine. I am looking for an _intuitive_ explanation. It keeps being said 'the identity is equivalent to PT', but it doesn't go both ways. PT certainly _applies_ for the given inner product (since PT is true of all IP spaces). Now if you said that weighted mean and variance are orthogonal norms (so PT applies) in an IP space with IP the weighted dot product, _that_ would be an intuitive explanation. – Mitch Jan 08 '17 at 19:29
  • @MatthewGunn Yes, I personally lack facility with the concept of random variable and sample space and how it matches my intuition of samples. – Mitch Jan 08 '17 at 19:31
  • Can you comment on my answer? The appropriateness of my interpretation of notation, etc. Also, how your interpretation (and I think equivalently mine) generalize? – Mitch Jan 12 '17 at 17:07
  • You can sometimes get back orthogonality in the "high school geometry" sense as follows: if you get 1 with probability 0.75 and 2 with probability 0.25, instead of working with X = [1 2] and having this special inner product with P = [0.75 0.25], just let X = [1 1 1 2] (or X = [1 2 1 1], etc., as long as you're consistent) – user3391564 Jan 03 '19 at 09:36
9

I will go for a purely geometric approach for a very specific scenario. Let us consider a discrete valued random variable $X$ taking values $\{x_1,x_2\}$ with probabilities $(p_1,p_2)$. We will further assume that this random variable can be represented in $\mathbb{R}^2$ as a vector, $\mathbf{X} = \left(x_1\sqrt{p_1},x_2\sqrt{p_2} \right)$. enter image description here

Notice that the length-square of $\mathbf{X}$ is $x_1^2p_1+x_2^2p_2$ which is equal to $E[X^2]$. Thus, $\left\| \mathbf{X} \right\| = \sqrt{E[X^2]}$.

Since $p_1+p_2=1$, the tip of vector $\mathbf{X}$ actually traces an ellipse. This becomes easier to see if one reparametrizes $p_1$ and $p_2$ as $\cos^2(\theta)$ and $\sin^2(\theta)$. Hence, we have $\sqrt{p_1} =\cos(\theta)$ and $\sqrt{p_2} = \sin(\theta)$.

One way of drawing ellipses is via a mechanism called Trammel of Archimedes. As described in wiki: It consists of two shuttles which are confined ("trammelled") to perpendicular channels or rails, and a rod which is attached to the shuttles by pivots at fixed positions along the rod. As the shuttles move back and forth, each along its channel, the end of the rod moves in an elliptical path. This principle is illustrated in the figure below.

Now let us geometrically analyze one instance of this trammel when the vertical shuttle is at $A$ and the horizontal shuttle is at $B$ forming an angle of $\theta$. Due to construction, $\left|BX\right| = x_2$ and $\left| AB \right| = x_1-x_2$, $\forall \theta$ (here $x_1\geq x_2$ is assumed wlog).

enter image description here

Let us draw a line from origin, $OC$, that is perpendicular to the rod. One can show that $\left| OC \right|=(x_1-x_2) \sin(\theta) \cos(\theta)$. For this specific random variable \begin{eqnarray} Var(X) &=& (x_1^2p_1 +x_2^2p_2) - (x_1p_1+x_2p_2)^2 \\ &=& x_1^2p_1 +x_2^2p_2 - x_1^2p_1^2 - x_2^2p_2^2 - 2x_1x_2p_1p_2 \\ &=& x_1^2(p_1-p_1^2) + x_2^2(p_2-p_2^2) - 2x_1x_2p_1p_2 \\ &=& p_1p_2(x_1^2- 2x_1x_2 + x_2^2) \\ &=& \left[(x_1-x_2)\sqrt{p_1}\sqrt{p_2}\right]^2 = \left|OC \right|^2 \end{eqnarray} Therefore, the perpendicular distance $\left|OC \right|$ from the origin to the rod is actually equal to the standard deviation, $\sigma$.

If we compute the length of segment from $C$ to $X$: \begin{eqnarray} \left|CX\right| &=& x_2 + (x_1-x_2)\cos^2(\theta) \\ &=& x_1\cos^2(\theta) +x_2\sin^2(\theta) \\ &=& x_1p_1 + x_2p_2 = E[X] \end{eqnarray}

Applying the Pythagorean Theorem in the triangle OCX, we end up with \begin{equation} E[X^2] = Var(X) + E[X]^2. \end{equation}

To summarize, for a trammel that describes all possible discrete valued random variables taking values $\{x_1,x_2\}$, $\sqrt{E[X^2]}$ is the distance from the origin to the tip of the mechanism and the standard deviation $\sigma$ is the perpendicular distance to the rod.

Note: Notice that when $\theta$ is $0$ or $\pi/2$, $X$ is completely deterministic. When $\theta$ is $\pi/4$ we end up with maximum variance.

jkt
  • 513
  • 3
  • 14
  • 1
    +1 Nice answer. And multiplying vectors by the square of the probabilities is a cool/useful trick to make the usual probabilistic notion of orthogonality look orthogonal! – Matthew Gunn Jan 05 '17 at 20:18
  • Great graphics. The symbols all make sense (the trammel describing an ellipse and then the Pythagorean Thm applies) but somehow I'm not getting _intuitively_ how it gives an idea of how 'magically' it relates the moments (the spread and center. – Mitch Jan 08 '17 at 16:51
  • consider the trammel as a process that defines all the possible $(x_1,x_2)$ valued random variables. When the rod is horizontal or vertical you have a deterministic RV. In the middle there is randomness and it turns out that in my proposed geometric framework how random a RV (its std) is exactly measured by the distance of the rod to the origin. There might be a deeper relationship here as elliptic curves connects various objects in math but I am not a mathematician so I cannot really see that connection. – jkt Jan 08 '17 at 21:24
3

You can rearrange as follows:

$$ \begin{eqnarray} Var(X) &=& E[X^2] - (E[X])^2\\ E[X^2] &=& (E[X])^2 + Var(X) \end{eqnarray} $$

Then, interpret as follows: the expected square of a random variable is equal to the square of its mean plus the expected squared deviation from its mean.

Starz
  • 432
  • 1
  • 3
  • 11
1

Sorry for not having the skill to elaborate and provide a proper answer, but I think the answer lies in the physical classical mechanics concept of moments, especially the conversion between 0 centred "raw" moments and mean centred central moments. Bear in mind that variance is the second order central moment of a random variable.

S. Diaxo
  • 23
  • 8
1

The general intuition is that you can relate these moments using the Pythagorean Theorem (PT) in a suitably defined vector space, by showing that two of the moments are perpendicular and the third is the hypotenuse. The only algebra needed is to show that the two legs are indeed orthogonal.

For the sake of the following I'll assume you meant sample means and variances for computation purposes rather than moments for full distributions. That is:

$$ \begin{array}{rcll} E[X] &=& \frac{1}{n}\sum x_i,& \rm{mean, first\ central\ sample\ moment}\\ E[X^2] &=& \frac{1}{n}\sum x^2_i,& \rm{second\ sample\ moment\ (non-central)}\\ Var(X) &=& \frac{1}{n}\sum (x_i - E[X])^2,& \rm{variance, second\ central\ sample\ moment} \end{array} $$

(where all sums are over $n$ items).

For reference, the elementary proof of $Var(X) = E[X^2] - E[X]^2$ is just symbol pushing: $$ \begin{eqnarray} Var(X) &=& \frac{1}{n}\sum (x_i - E[X])^2\\ &=& \frac{1}{n}\sum (x^2_i - 2 E[X]x_i + E[X]^2)\\ &=& \frac{1}{n}\sum x^2_i - \frac{2}{n} E[X] \sum x_i + \frac{1}{n}\sum E[X]^2\\ &=& E[X^2] - 2 E[X]^2 + \frac{1}{n} n E[X]^2\\ &=& E[X^2] - E[X]^2\\ \end{eqnarray} $$

There's little meaning here, just elementary manipulation of algebra. One might notice that $E[X]$ is a constant inside the summation, but that is about it.

Now in the vector space/geometrical interpretation/intuition, what we'll show is the slightly rearranged equation that corresponds to PT, that

$$ \begin{eqnarray} Var(X) + E[X]^2 &=& E[X^2] \end{eqnarray} $$

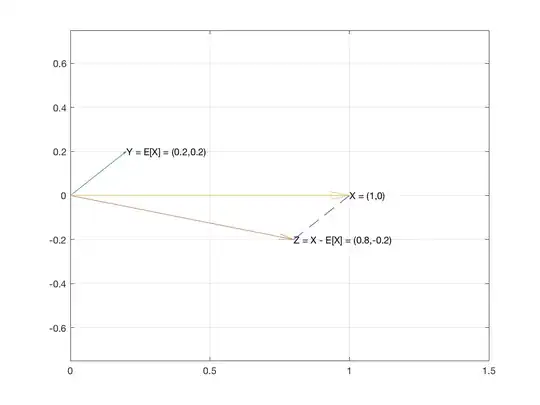
So consider $X$, the sample of $n$ items, as a vector in $\mathbb{R}^n$. And let's create two vectors $E[X]{\bf 1}$ and $X-E[X]{\bf 1}$.

The vector $E[X]{\bf 1}$ has the mean of the sample as every one of its coordinates.

The vector $X-E[X]{\bf 1}$ is $\langle x_1-E[X], \dots, x_n-E[X]\rangle$.

These two vectors are perpendicular because the dot product of the two vectors turns out to be 0: $$ \begin{eqnarray} E[X]{\bf 1}\cdot(X-E[X]{\bf 1}) &=& \sum E[X](x_i-E[X])\\ &=& \sum (E[X]x_i-E[X]^2)\\ &=& E[X]\sum x_i - \sum E[X]^2\\ &=& n E[X]E[X] - n E[X]^2\\ &=& 0\\ \end{eqnarray} $$

So the two vectors are perpendicular which means they are the two legs of a right triangle.

Then by PT (which holds in $\mathbb{R}^n$), the sum of the squares of the lengths of the two legs equals the square of the hypotenuse.

By the same algebra used in the boring algebraic proof at the top, we showed that we get that $E[X^2]$ is the square of the hypotenuse vector:

$(X-E[X])^2 + E[X]^2 = ... = E[X^2]$ where squaring is the dot product (and it's really $E[x]{\bf 1}$ and $(X-E[X])^2$ is $Var(X)$.

The interesting part about this interpretation is the conversion from a sample of $n$ items from a univariate distribution to a vector space of $n$ dimensions. This is similar to $n$ bivariate samples being interpreted as really two samples in $n$ variables.

In one sense that is enough, the right triangle from vectors and $E[X^2]$ pops out as the hypotnenuse. We gave an interpretation (vectors) for these values and show they correspond. That's cool enough, but unenlightening either statistically or geometrically. It wouldn't really say why and would be a lot of extra conceptual machinery to, in the end mostly, reproduce the purely algebraic proof we already had at the beginning.

Another interesting part is that the mean and variance, though they intuitively measure center and spread in one dimension, are orthogonal in $n$ dimensions. What does that mean, that they're orthogonal? I don't know! Are there other moments that are orthogonal? Is there a larger system of relations that includes this orthogonality? central moments vs non-central moments? I don't know!

Mitch
  • 1,691
  • 2
  • 18
  • 33
  • I am also interested in an interpretation/intuition behind the superficially similar bias variance tradeoff equation. Does anybody have hints there? – Mitch Jan 12 '17 at 17:08
  • Let $p_i$ be the probability of state $i$ occurring. If $p_i = \frac{1}{n}$ then $\sum_i p_i X_i Y_i = \frac{1}{n} \sum_i X_i Y_i$, that is, $E[XY]$ is simply the dot product between $X$ and $Y$ divided by $n$. If $\forall_i p_i = \frac{1}{n}$, what I used as an inner product ( $E[XY] = \sum_i p_i X_i Y_i$) is basically the dot product divided by $n$. This whole Pythagorean interpretation still needs to you use the particular inner product $E[XY]$ (though it's algebriacly close to the classic dot product for a probability measure $P$ such that $\forall_i p_i = \frac{1}{n}$). – Matthew Gunn Jan 12 '17 at 18:01
  • Btw, the trick @YBE did is to define new vectors $\hat{x}$ and $\hat{y}$ such that $\hat{x}_i = x_i \sqrt{p_i}$ and $\hat{y}_i = x_i \sqrt{p_i}$. Then dot product $\hat{x} \cdot \hat{y} = \sum_i x_i \sqrt{p_i} y_i \sqrt{p_i} = \sum_i p_i x_i y_i = E[xy]$.The dot product of $\hat{x}$ and $\hat{y}$ corresponds to $E[xy]$ (which is what I used as an inner product). – Matthew Gunn Jan 12 '17 at 18:08