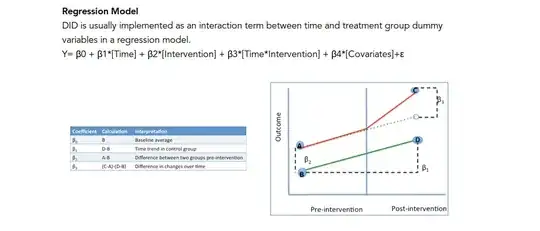
This is often shown as the setup and simple analysis for a difference-in-difference estimation. Lets say that the control series is significantly smaller than the treated series. Below this means the green line would be greatly shifted downward - but still similar trend as red (the primary assumption of d-i-d). Does the (C-A)-(D-B) still work if the outcome value for the series is not close to each other? It seems like we would need to use percentage change.
Here is an example. The d-i-d estimate is 963. It doesn't make sense though to me to adjust the increase in the treatment market by the change in the control when the sizes are so different. It seems like a better approach would be to look at the growth in control (20% here) and apply that to the treated: 1.2*1530 and then compare this against the actual of 2500. In this case the estimate would be 664.
It seems like we should compare the treated market growth to the % change in the control market because as is, we remove from the treated increase the absolute value of the control and that seems wrong, since the starting base for the control is so much lower. 7 units is 20% increase for the control, but is very small compared to the treated.