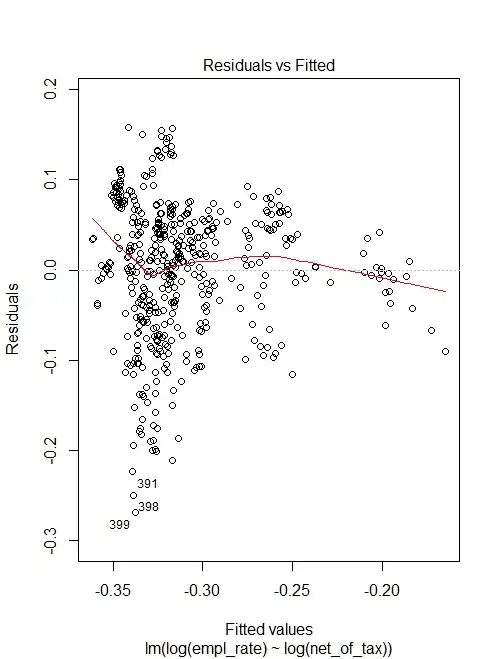
I am performing a simple linear regression with the lm() function to make statements about the association between the two variables. But I am not sure if my regression estimates and the t-test are correct due to the violations of assumptions (homoscedasticity and normal distribution of the error term)
My regression model looks as follows: log(employment rate) = a + e * log(net-of-tax), because I want to interpret the estimate as elasticity.
reg_test = lm(formula = log(empl_rate) ~ log(net_of_tax), data = dat)
The summary output looks like:
> summary(reg_test)
Call:
lm(formula = log(empl_rate) ~ log(net_of_tax), data = dat)
Residuals:
Min 1Q Median 3Q Max
-0.26905 -0.04372 0.00933 0.05167 0.15835
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.385486 0.007953 -48.47 <2e-16 ***
log(net_of_tax) -0.085839 0.008276 -10.37 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.07481 on 477 degrees of freedom
Multiple R-squared: 0.184, Adjusted R-squared: 0.1823
F-statistic: 107.6 on 1 and 477 DF, p-value: < 2.2e-16
Am I correct in assuming that:
- since heteroskedasticity does not bias the coefficient estimates it is possible to relax the assumption and just adjust the incorrect standard errors (e.g., using HC1), and
- because of the large sample size, the error terms can deviate from normality?