4

I'm trying to do a hypothesis testing and the result I'm getting is strange because the p value I get is greater than 1.

I'm using $p_0= 0.65$ and $\hat{p} = 0.60$.

To calculate $Z$ I'm using $(0.60-0.65)/\sqrt{0.65(1-0.65)/50} = -0.74$

In the $Z$ table I get: $0.2296$

Then $(1-0.2296) * 2$ (*2 because its a two tailed test) and the result is $1.54$.

Do you know where the problem is?

Glen_b
  • 257,508
  • 32
  • 553
  • 939
Chen
  • 53
  • 1
  • 1
  • 5
  • Can you show what your tables look like? (alternatively, if you google for normal tables can you find one that looks like yours?) – Glen_b Dec 21 '16 at 01:47
  • For exemple here: http://www.stat.purdue.edu/~mccabe/ips4tab/bmtables.pdf – Chen Dec 21 '16 at 02:06
  • 2
    The two-tailed test is about $|z|$, and if you use $|z|\geq{0}$ to get the "one-tailed p" then $p_2=2(1-p_1)$ will never exceed one. – GeoMatt22 Dec 21 '16 at 02:45
  • I have edited my answer to incorporate the change you made to the table lookup (which I didn't see you'd made when I posted). – Glen_b Dec 21 '16 at 04:21

1 Answers1

8

It appears that you're doing a hypothesis test of proportions.

You have $H_0: p = 0.65$ vs $H_1: p\neq 0.65$, using a normal approximation to the distribution of the standardized proportion (corresponding to a normal approximation to the binomial).

In a sample of $n=50$ you have an observed number of successes of $30$, giving a sample proportion of $0.6$.

The total area you want for your two tailed p-value is this:

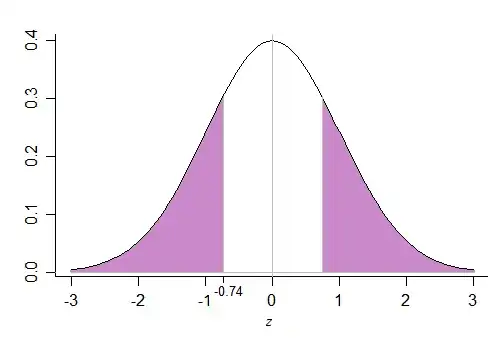
Normal density with two-tail area corresponding to z=-0.74 marked in

You can do that by finding the area to the left of -0.74 and then doubling it.

The area to the left of $-0.74$ can be found directly in the tables you have, but you didn't look them up correctly.

[Your question now shows this calculation correctly, but at the time I was composing this part of the answer it didn't and I didn't notice you had changed that some time after I posted my answer. I have left the discussion of the incorrect table-lookup here even though you understand how to do it now, because it may nevertheless prove useful to the next person.]

You (originally) looked up -0.07 (you looked at the row for -0.0 and then the column for .07) but you need to look up the row for -0.7, and then the column for 0.04:

Normal tables showing how to look up -0.74

That gives 0.2296 (as your question now shows, so you understand up to here now).

You then subtracted your area from 1 and doubled. In this case you should simply double the area to get the area in both tails. [The subtract-from-1 works with the table you have for $z$ values that are non-negative, to give upper-tail areas, which you would then double to get two-tails, but you are not in a situation here where $z\geq 0$, so you're not calculating an upper tail area.]

I'd strongly advise always drawing a diagram like the one above so that you can see the calculation you need to be doing.

[Alternatively, for a two-tailed test such as this, you could follow GeoMatt's advice in comments of always looking up the absolute value of $z$, (by dropping the sign when it's negative) and then doing the "subtract from 1 then double" action that otherwise works for $z>0$.]

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • Thanks for your answer. So the p value is equal to 0.46 and we cant reject the null hypotesis. I just have one doubt because you said that my hypoteses definition was ho equal to 65 and h1different from 65, but I assum that h0 was less or equal to 0.65 and the h1 was bigger than 0.65, the process it is the same right? – Chen Dec 21 '16 at 21:59
  • No the process is a bit different for a one-tailed test, you only look at one tail (but be careful -- you have to make sure you look in the correct direction!) . You didn't state your hypotheses so I was forced to guess from what you did (which was double your tail area when you showed your calculation, implying you were doing a two-tailed test). .You just look in the correct direction in your null distribution (toward the direction of the alternative from your observed Z) to find the area (don't double it). Note that this would mean looking to the right of -0.74 (subtract tabled value from 1) – Glen_b Dec 21 '16 at 23:22
  • But in this case as i have h0 with <= and h1 with >, so its not also a two tailed test? – Chen Dec 22 '16 at 00:21
  • No, it's a one tailed test, as I said. Look at the alternative, which includes only one tail. – Glen_b Dec 22 '16 at 00:32