Information about the data
For this study, I would like to statistically test how the total length of sparrows affects their survival. Consider here one of the characteristics of the sparrows recorded was total length, which is assumed to be normally distributed.
Information regarding the data:
In a group of 21 surviving sparrows, the variance of the total length was 11.05 mm2.
In a group of 28 sparrows that subsequently died, the variance of the total length was 15.07 mm2.
The µ of the total length of sparrows that survived was 157.4 mm2
The mean µ of the total length of sparrows that subsequently died was 158.4 mm2
Problems to solve:
I am unsure if I have understood the concepts correctly underpinning how to: -
- Read quantile tables properly for Chi-square and F distributions
- Calculate 95 % confidence intervals
If this is possible, I would be incredibly grateful if anyone could please check the answers to the questions stated below by providing advice. Many thanks in advance for your help.
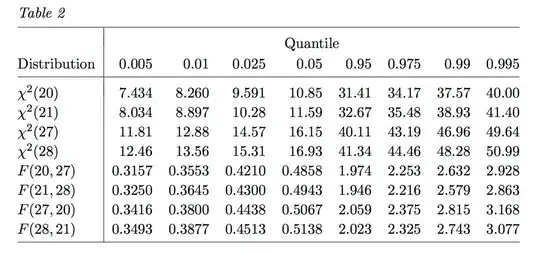
Quantile Table
Question 1
I would like to establish if the variance of the length of survivors is compatible with the calculated confidence interval for non-survivors?
Sample unit = total length of sparrows
- Calculate the 95 % CI for the variance of 15.07 mm2 for total length of 28 sparrows that did not survive
0.975 and 0.025 Chi-Square (χ2) distribution for non-survivors (n=28) inferred from the quantile table:
- χ2(28)(0.025) = 15.31
- χ2(28)(0.975) = 44.46
Calculate Confidence Intervals:
- σ² (non-survivors) = 15.07 mm2
Confidence interval = (n-1) * σ² / χ2
- 0.975 CI = (28-1)*(15.07)/15.31 = 26.58
- 0.05 CI = (28-1)*(15.07)/44.46 = 9.15
The variance for survivors (n=21) is 11.05 mm2
The variance of the length of survivors (i.e 11.05 mm2) is compatible with the confidence interval range for non-survivors (0.975 = 26.58, 0.025 = 9.15) Therefore, from these calculations we are 95 % confident that the true population variance for survivors (n=21) does fall within the confidence intervals for non-survivors (n=28).