4

For an assignment, I have used iPython to create the dendrogram below, using Ward's method and Euclidean distance, from the following data: $$a=(0,0)$$ $$b=(1,2)$$ $$c=(3,4)$$ $$d=(4,1)$$ $$e=(2,2)$$ 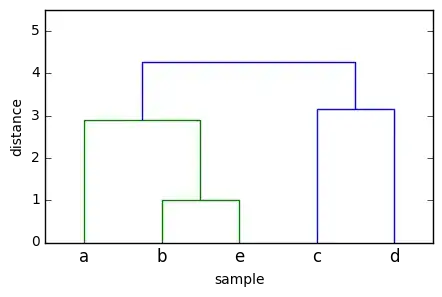enter image description here where dist({a},{b,e}) = 2.88, and dist({a,b,e},{c,d})=4.27.

How are these values derived? I've tried using the recursive method given here, but am not getting the same results.

Any help muchos appreciated.

I know that dist(a,b)=$\sqrt{5}$, dist(a,e)=$\sqrt{8}$, so using the formula on the wikipedia page, I have dist({a},{b,e})=$\frac{2}{3}\sqrt{5} + \frac{2}{3}\sqrt{8} - \frac{1}{3} = 3.04$. Where am I going wrong?

Harr
  • 61
  • 5
  • Please add the `[self-study]` tag & read its [wiki](http://stats.stackexchange.com/tags/self-study/info). Then tell us what you understand thus far, what you've tried & where you're stuck. We'll provide hints to help you get unstuck. – gung - Reinstate Monica Dec 15 '16 at 14:26
  • done - btw this isn't a homework question, it's a question I've put together myself for a quiz – Harr Dec 15 '16 at 14:35
  • The Talk page at the wikipedia article discusses all the necessary details. Please see also in http://stats.stackexchange.com/a/217742/3277. And remember Ward's method operates on _squared_ distances. – ttnphns Dec 15 '16 at 15:17

2 Answers2

3

Having banged my head on the wall for the last 2 hours on this, I feel your pain.

The result is the square root of the increase in within-cluster sum of squares (vs. cluster means), multiplied by $\sqrt{2}$ for some reason.

$$ \sqrt{ 2 \left( \sum_{i \in (C_1 \cup C_2)} \lVert \vec x_i - \bar x_{C_1 \cup C_2} \rVert^2 - \sum_{i \in (C_1)} \lVert \vec x_i - \bar x_{C_1} \rVert^2 - \sum_{i \in (C_2)} \lVert \vec x_i - \bar x_{C_2} \rVert^2 \right) } $$

For $C_1 = \{ a, b, e \}, C_2 = \{ c,d \}$ the result is $4.27$ as you require.

As for how exactly they are derived, depends on the specifics of the algorithm in use.

Michael Hore
  • 31
  • 2
0

The right is: $$dist(\{a\},\{b,e\})=\left(\frac23\right)\cdot 5+\left(\frac23\right)\cdot 8–\frac13\cdot 1=\frac{25}3$$ Then $$dist(\{a\},\{b,e\})=\sqrt{\frac{25}3}=2.88$$

Siong Thye Goh
  • 6,431
  • 3
  • 17
  • 28
guest
  • 1