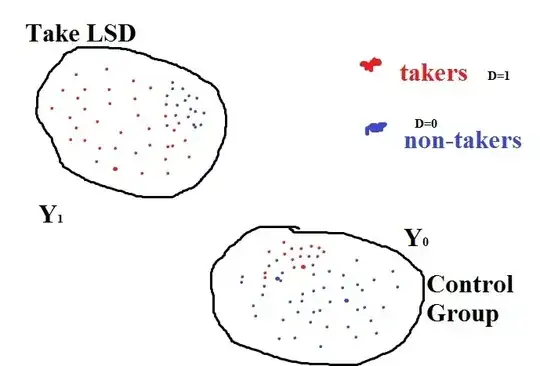
I have some problems understanding the difference between ATE and ATET and the Selection Bias. To explain what my understanding is I have done the following representation so you can correct me:
We want to see the effect of taking LSD, to do so we have a Group to which we assign the "treatment" so $D=1$ and a group which has no treatment assigned so $D=0$. On the top left corner we can see $Y_{1i}$ and on the right bottom corner $Y_{0i}$. The problem comes now, as far as I can understand because there is no randomization (?) in the sample we have that some guys in the control group that take LSD because they are drug-abusers (red dots) ($E[Y_{0i}|D=1]$). In addition some other guys in the treatment group do not do LSD because they are afraid ($E[Y_{1i}|D=0]$). So:
$ATE = E[Y_{1i}|D=1] - E[Y_{0i}|D=1] + E[Y_{0i}|D=1] - E[Y_{0i}|D=0]$
Where the first two terms are ATE and the last two are Selection Bias.
Why $E[Y_{0i}|D=1]$ is not observable? Is this explanation correct? Why if we apply randomization in the treatment we manage to get $E[Y_{0i}|D=1] - E[Y_{0i}|D=0] = 0$ ?