Given: $X \sim \text{Triangular}(-a,m,a)$ with pdf $f(x)$:

(source: tri.org.au)
where parameter $m$, instead of being fixed, is itself a random variable. In particular, $M \sim \text{Uniform}(-a,a)$, with pdf $g(m)$:

(source: tri.org.au)
Then, we seek the parameter mixture distribution $E_{g }\big[\;f (x \; \big | \;M =m )\big]$, which has pdf say $h(x)$:

(source: tri.org.au)
where I am using the Expect function from the mathStatica package for Mathematica to automate the calculation. The domain of support is, of course, $(-a,a)$.
To illustrate, here is a plot of the pdf $h(x)$, as parameter $a$ varies:
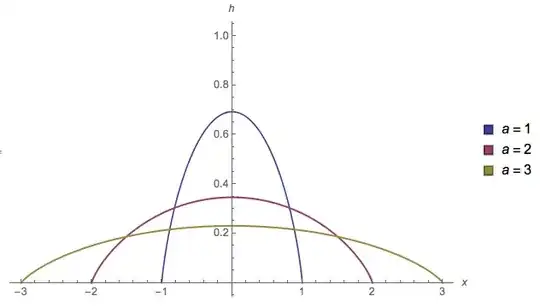
(source: tri.org.au)
The cdf $P_h(X<x)$ is:
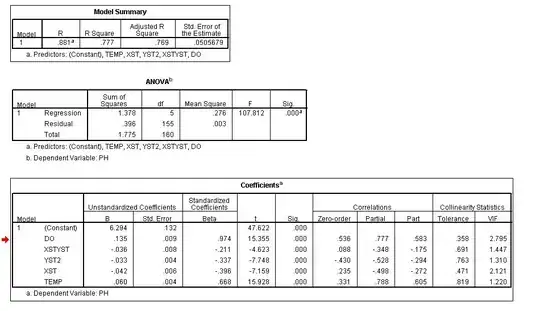
(source: tri.org.au)
Comparison to semi-circle distribution
The following diagram compares the pdf of the exact solution $h(x)$ to the semicircle pdf that the OP refers to. The pdf $h(x)$ is somewhat more peaked than the semi-circle:
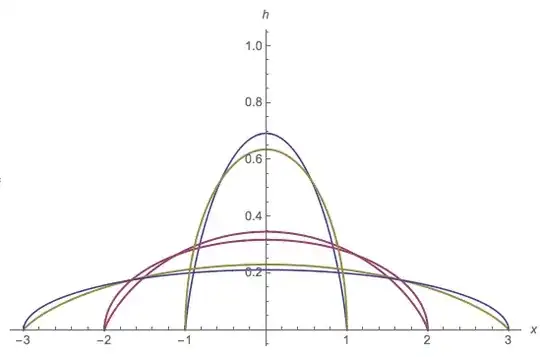
(source: tri.org.au)
Comparison to POWER semi-circle distribution
While the functional form is different, one can approximate the pdf $h(x)$ extremely well with a power semi-circle distribution of form:
$$ \phi(x) = k \left(a^2-x^2\right)^{3/4}$$
where $k = \frac{\Gamma \left(\frac{9}{4}\right)}{\left(\sqrt{\pi } a^{5/2}\right) \Gamma \left(\frac{7}{4}\right)}$
The fit is so good that one can barely see any perceptible difference:
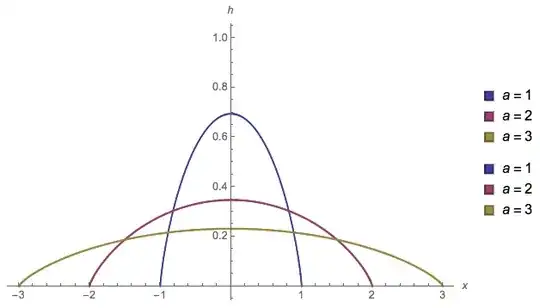
(source: tri.org.au)






