I am reading from Daphne Koller's book and I don't understand how she find this probability:
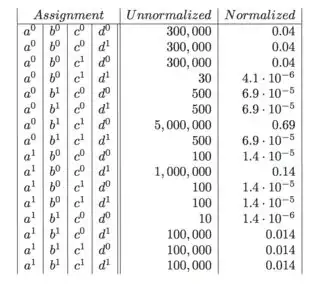
She provides this table (on page 105):
and claims that "For example, by summing out A, C, and D, we obtain P($b^{1}$) ≈ 0.732 and P($b^{0}$) ≈ 0.268" which is understandable to me. Then she says that: "On the other hand, if we now observe that Charles does not have the misconception ($c^{0}$), we obtain P($b^{1} | c^{0}$) ≈ 0.06." This is on the end of page 105.
I don't get it how this 0.06 comes up. Any help much appreciated.
the book: Probabilistic Graphical Models: Principles and Techniques, by D. Koller and N. Friedman, MIT Press, 2009.