I want to run a regression where the dependant variable (DV) is the amount of funding (in USD) obtained by startups. Naturally the DV contains a lot of zero's (~55%) and has a continuous distribution for y>0.
In general my understanding is that the Tobit model (or a variation of it) is approriate to model this DV.
Although reading and discussing now for months I still struggle to get my head around the exact difference between the standard Tobit (1958) model, the two-part extensions proposed by Cragg (1971) and the Tobit Type 2 model, e.g., represented by Heckmann (1974, 1976, 1979). My current understanding is that all models could be in theory applicable with varying pros and cons and potential reasons why not to use them at all (depending on the exact characteristics of the data set).
Why I excluded the standard Tobit model
For my application I excluded the standard Tobit model as it only allows both processes to be governed by the same variables for which also only one coefficient is reported. Hence, the effect of a certain variable cannot have a different sign in the selection and outcome equation (which is though sometimes the case).
Tobit Type 2 (or Heckmann selection model) vs. two-part model (Cragg)
My understanding so far is that the key difference between the 2 models is the fact that two-part models assume only true zeros, whereas Tobit Type 2 accounts also (or only?) for unobserved zeros (e.g., people who generally do not smoke are a 0 and people who generally smoke but at a certain point of time cannot afford to smoke are a 0 as well)
This, however, is not entirely true as Cragg (1971) originally also proposed a double hurdle model where 2 hurdles have to be overcome before positive values of y are observed: "First, a positive amount has to be desired [(i.e., I am a smoker or not)]. Second, favourable circumstances have to arise for the positive desire to be carried out [(i.e., I am a smoker and I have sufficient funds to afford smoking)]".
I think this means that the Tobit Type II accounts for both types of zeros (or only unobserved?) in the first selection equation and the outcome equation is truncated at y>0, the single hurdle Cragg model only accounts for true zeros in the selection equation and the double-hurdle Cragg model accounts for 'unobserved' zeros during the selection and 'true' zeros during the outcome equation.
Questions
Is my statement about the three models correct? And what does this exactly mean? Are the sources of zeros the only/main decision criteria? If so, this would mean for me with regard to my data: startups decide to apply for funding or not (first source of zeros -> unobserved), subsequently the market decides to supply funding or not (second source of zeros -> observed) and, in the positive case, how much (y > 0) -> Cragg's double hurdle model (the real 'double' hurdle model which is often wrongly mistaken for the single hurdle model)
Irrespectively of my (potentially wrong) conlusion: What are the key decision criteria I should consider/discuss when deciding about what type of model to use (Tobit Type 2 (Heckmann) model or a two-part model (either single hurdle (all zeros are true zeros) or double hurdle (zeros can arise at selection and consumption))? Is there more than 'just' the source of the zeros?
Additional information
This paper (which is a great read! Brad R. Humphreys, 2013) and especially one of its key graphics 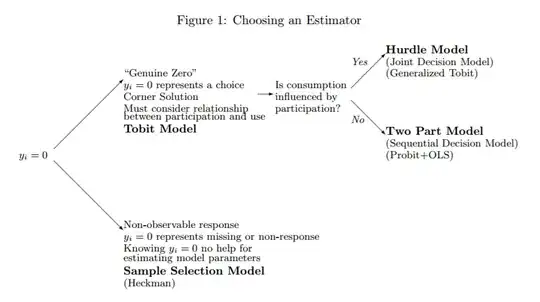 highlights the difference between unobserved zeros (i.e., missing data, companies not looking for funding) and observed zeros (i.e., investors providing funding or not) very well. It also provides guidance on which models to use, but unfortunately, does not provide a solution for data where both types of zeros are present at the same time.
highlights the difference between unobserved zeros (i.e., missing data, companies not looking for funding) and observed zeros (i.e., investors providing funding or not) very well. It also provides guidance on which models to use, but unfortunately, does not provide a solution for data where both types of zeros are present at the same time.
Potential solution
After digging deeper I found two papers that offer a statistical solution to exactly what I am looking for:
- Blundell, Richard and Meghir, Costas, (1987), Bivariate alternatives to the Tobit model, Journal of Econometrics, 34, issue 1-2, p. 179-200. (http://sites.psu.edu/scottcolby/wp-content/uploads/sites/13885/2014/07/Blundell1987_Bivariate-alternatives-to-the-tobit-model.pdf) describe a double hurdle model that assumes dependence. For an application see Blundell, Richard, Ham, John and Meghir, Costas, (1987), Unemployment and Female Labour Supply, Economic Journal, 97, issue 388a, p. 44-64.
- Another solution is offered by Moulton, Lawrence H., and Neal A. Halsey. “A Mixture Model with Detection Limits for Regression Analyses of Antibody Response to Vaccine.” Biometrics, vol. 51, no. 4, 1995, pp. 1570–1578. www.jstor.org/stable/2533289 who describe a Bernoulli/Lognormal Mixture Model for Censored Data that also accounts for both types of zeros.
Unfortunately I couldn't find any trustworthy implementation in Stata or R (there is a package called mhurdle, but it appears not to be working well with weights and throwing random errors...)
Any comments or further ideas?