0

The following link describes the Bayes weighted average with an example.

$$S = wR + (1-w)C$$

where
$S$ = score of the restaurant
$R$ = average of user ratings for the restaurant
$C$ = average of user ratings for all restaurants
$w$ = weight assigned to $R$ and computed as $v/(v+m)$, where $v$ is the number of user ratings for that restaurant, and $m$ is average number of reviews for all restaurants.

The example mentioned is

Restaurant A has 100 opinions with an average rating of 4.5
Restaurant B has 1 opinion with an average rating of 5

The grades are recalculated using the above formula. However I have the following question:

Q1) How is the value of $m = 40$ and $c = 4.2$ derived? As a follow up of the above question: Shouldn't the value of $m$ be $(100+1)/2 = 50.5$ and the value of $C$ be $(4.5+5)/2 = 4.75$?

Q2) Are the final weighted scores on a scale of 1-5 ?

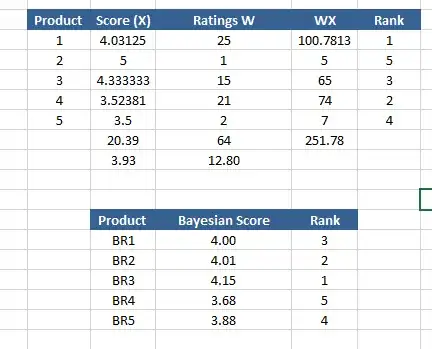
Update as of 06/12/2016 As a follow up to the link provided by tim and my understanding of the bayes weighted average, i have proposed an example with calculations. Please find attached the image.I have 2 questions A&B with respect to the image attached.

There are 5 products only each with their mean score and no of ratings

I have used the following formula to calculate the scores. Its the same formula posted earlier but i found this easier to implement. b(r) = [ W(a) * a + W(r) * r ] / (W(a) + W(r)]

where r = average rating for an item W(r) = weight of that rating, which is the number of ratings a = average rating for the entire data set of 5 products. W(a) = weight of that average, which is the average number of ratings for all the 5 products, b(r) = new bayesian rating

QA)The average rating for all products SUM(WX)/SUM(W) = 251.78/64 = 3.93. I took a weighted mean instead of an arithmetic mean. The average number of ratings for all W(a)= 64/5 = 12.80. I have set m = 12.80 on the observation that 70 % of the products(data points with regards to the number of ratings fall above this value) .

Is this value optimal ? Does it need to change dynamically each time the total avg number of ratings changes ?

QB)Based on the bayes score calculations,

Why is BR2 (4.01) which has only 1 rating with a mean score of 5/5 still ranked higher than BR1 (4.00) which has 25 ratings with a mean score of 4.03/5 and BR4 (3.68) which has 21 ratings with a mean score of 3.52 ?

Please find attached the image Bayes

Narayanan
  • 79
  • 3
  • 8
  • See here http://stats.stackexchange.com/a/226413/35989 – Tim Nov 30 '16 at 19:52
  • @tim. Thanks for sharing the link. Im trying to understand the concept in a simple manner so that i can apply to my statistics class cases. Case 1 compares five products only each with an average rating and number of ratings. Case 2 compares 5 products but the number of estimated products forming part of the same product segment is 15. I'm tring to figure out a standard m and c vaue to be used in both the case. Also the ratings are on a scale of 1-5. That puts my 2nd question in focus. – Narayanan Dec 01 '16 at 05:37
  • @tim Since i didnt uderstand Bayes well enough till now, i proposed another method. However this has issues. The link is here. http://stats.stackexchange.com/questions/247221/recalculate-ratings – Narayanan Dec 01 '16 at 05:51
  • Your question was closed for a reason (please see the comment for closure). Please **do not** post your question again because previous one was closed. Instead you should edit your question for it to be on-topic and answerable in here. – Tim Dec 02 '16 at 12:47
  • @ tim i have deleted the latest question. – Narayanan Dec 02 '16 at 12:53
  • @tim please take note of the updates. Kindly give in your feedback,Thanks. – Narayanan Dec 05 '16 at 12:29

1 Answers1

2

Q1) How is the value of $m = 40$ and $c = 4.2$ derived? As a follow up of the above question: Shouldn't the value of $m$ be $(100+1)/2 = 50.5$ and the value of $C$ be $(4.5+5)/2 = 4.75$?

Neither $m$ nor $c$ were "derived", those are some known values. This is actually said in the blog post you refer to:

Let’s first assume that the average of user ratings for all restaurants (C) is 4.2 and the average number of reviews for all restaurants (m) is 40.

As about your second question

Q2) Are the final weighted scores on a scale of 1-5 ?

Yes. $R$ in on 1-5 scale, $C$ is on 1-5 scale, $w$ is in $[0,1]$, so $w + (1-w)=1$ and the weighted mean cannot be outside the 1-5 range.

As about your edits, I don't see what is the question you want to ask. Actually the blog post you refer to tells everything about this formula and gives detailed example. There is nothing more that could be said. Also there is no deeper math or statistical rationale behind it, it is simply a weighted average of all scores and the particular rating.

Tim
  • 108,699
  • 20
  • 212
  • 390
  • @Thanks for the answer with respect to my question related to the link i posted. With reference to your link, I have posted 2 examples with results and questions that follow them. I have edited the question with questions a b and c. kindly have a look. – Narayanan Dec 05 '16 at 13:53
  • @Narayanan I do not think that there is anything to add. The formula is very simple and needs only a primary school arithmetic. The blog post you refer to describes it in details giving multiple examples. There is nothing more that can be said. If you are looking for someone to check your Excel calculations, then sorry, but it's off-topic in here. – Tim Dec 05 '16 at 17:46
  • I do understand that the formula is simple and primary school arithmetic. But my question is still isn't answered. How do I determine what values I assign to m&c. Thanks for all your help :-) – Narayanan Dec 05 '16 at 18:01
  • @Narayanan ...but you yourself said what they are: m is average number of reviews for all restaurants and C is average rating for all restaurants. – Tim Dec 05 '16 at 18:03
  • @ Tim. True. But what I've understood and assumed in my last update is that m & c needs to be an arbitrary number. That's the reason why I wrote an example so that I can it can be validated for correctness. I would suggest just have a look at my update. You'll get my drift. – Narayanan Dec 05 '16 at 18:09
  • @Narayanan ...then I do not understand what is your question. In the link you refer to: m is average number of reviews for all restaurants and C is average rating for all restaurants. There's nothing more to add. I'm cutting off this discussion because this leads nowhere. The answers to your questions are given in the link you provided. – Tim Dec 05 '16 at 18:18
  • The question has been updated with 2 questions A & B. Kindly have a look and give me your feedback. – Narayanan Dec 06 '16 at 08:18
  • @Narayanan But your questions are unanswerable... (QA): It is impossible to say if it is or is not optimal "out of the void". Optimal given what criteria? In what sense? (QB): there is no answer for the "why" question. The values are as so *because* they follow from the used formula. If you want to check how different outcomes are related to different starting values you can easily use different values for c and m and check what happens. There is no answer for the "why" question. – Tim Dec 06 '16 at 08:50
  • QA) The logic with m = 12.80 is with reference to your example on IMDb that 80 percent if the data point fall above this value. I used the same logic because I found it to be correct. It's mentioned in the post that I have updated. – Narayanan Dec 06 '16 at 09:22
  • QB)I guess the question is clear enough. – Narayanan Dec 06 '16 at 09:23
  • i have updated the description of the question as well as some changes in the main text. – Narayanan Dec 07 '16 at 12:39