I am moderately familiar with frequentist hierarchical modeling, structural equation modeling, and hierarchical structural equation modeling. I am also moderately familiar with bayesian graphical networks, though less so.
I also have an amateur level of experience/understanding with bayesian versions of standard glm models.
For some time, I have wanted to make the transition to fully Bayesian modeling and I have a current modeling problem that I have decided to use as a transition case. However, I have not been able to find examples of model implementations that map easily onto my problem, so I am hoping to receive either specific comments on my general modeling problem, suggestions for modeling frameworks, and/or suggestions for further reading.
Below, I describe the problem I am trying to model (using STAN):
The Model:
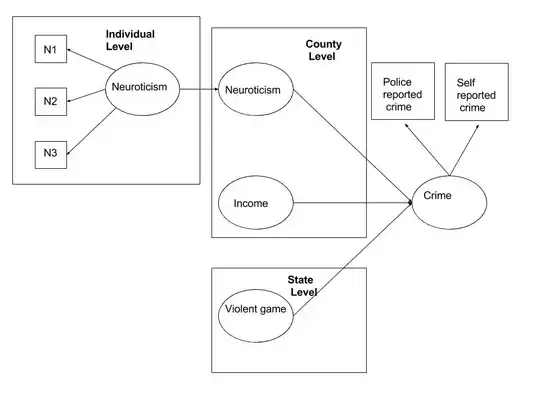
The dependent variable is county-level crime rate $crime$. Let's assume it is a latent variable estimated from police report data for the county and regionally representative self-report data that is sampled to match each county's demographic profile. Or, for the sake of simplicity, just assume that I am interested in modeling a latent estimate of crime.
I would like to model county-level crime rate as a function of the following blocks of predictors:
Block 1. A set of representative county-level demographic estimates (e.g. population, gender ratio, ethnicity composition, etc). Let's just limit the variables to median income $income$.
Block 2. A non-representative set of k individual level latent attitude measurements estimated from a set of observed survey items. These attitude measurements have been extracted from a large online survey that contains some geocoded data that has been mapped to counties. For each county, the minimum data point (as the data is currently structured) is bounded at one. For simplicity, let's limit this to one latent variable, neuroticism $nuerotic$ with indicators $N_1$, $N_2$, and $N_3$.
Block 3. A set of state-level variables that I would like to explore but for which there are no county level estimates. I'll limit this to one variable, also: purchase rate for top 100 violent video games $violentGame$.
If you can forgive the wretched SEM style graph, I would like to estimate the following model:
The model that I am primarily interested is described roughly by the following formula:
$crime_{c} = [\beta_0 + u_{0c}] + [\beta_1*income_c + u_{1c}] + [\beta_2*nuerotic_c + u_{2c}] + [\beta_3*violentGame_c + u_{3c}] + \epsilon_c$
That is, I am primarily interested in the county-level effects; I would like to estimate a random intercept for county-level crime and random effects for income, nueroticism, and violent game purchase, as well as the corresponding fixed effects.
However, ideally I would like to represent the uncertainty of individual-level measures of neuroticism and county-level measures of neuroticism.
Further, because some counties have sparse coverage for neurotic, I think I need to use partial pooling (as in this paper http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0141854#sec020) in order to make more stable county-level estimates.
Finally, based on my currently very limited reading about spatial analysis, I wonder if I should really be estimating a CAR model, or at least including adjecency information in some form.
Given the presence of within-subject items (e.g. $N_1$), individual level estimates of $neuroticism$, county-level estimates, and state-level estimates, I guess this is a four-level model. Ultimately, I am concerned that after the considerable time it will take me to learn how to construct this model, I will realize that it has too many parameters, won't converge for some other reason, or is ultimately not a suitable approach. I know this is a too-vague question, but I am hoping someone can tell me, 'no, don't do it like that, do it like this,' or, 'yes, this is a reasonable approach approach.'
Further, if anyone is aware of any code implementing hierarchical bayesian models with latent independent variables, I would appreciate a link. Finally, if anyone is aware of similar models in the domain of spatial analysis, I would appreciate links or thoughts.
I am currently learning stan (in R), and I would like to implement this model using stan. Recently, a few stan tricks have made estimating CAR releatively efficient. However, I am also aware of GeoBUGS -- perhaps that would be a more expedient route?
I understand this is all rather scattered and I apologize for that. However, most of my experience is with frequentist statistics in the social psychology domain and machine learning. As I am trying to bring together several areas that are new to me (spatial analysis and hierarchical bayesian modeling with latent independent and dependent variables), I am hoping that someone might be able to offer explicit advice or materials that apply directly to my problem.