A general idea is that you should repeat the simulation until the results converge. An easy but illustrative example of this is that we want to see if the R function rbinom is accurate in simulating a coin toss with a given probability. We will simulate one coin toss 10000 times, and plot the percentage of heads against the number of coin tosses:
set.seed(1)
n <- 10000
result <- NULL
percent <- NULL
for (i in 1:n) {
result[i] <- rbinom(1,1,0.5)
percent[i] <- sum(result)/i
}
plot(seq(1:10000),percent, type="l")
abline(0.5, 0, lty=2)
The resulting plot looks like this:
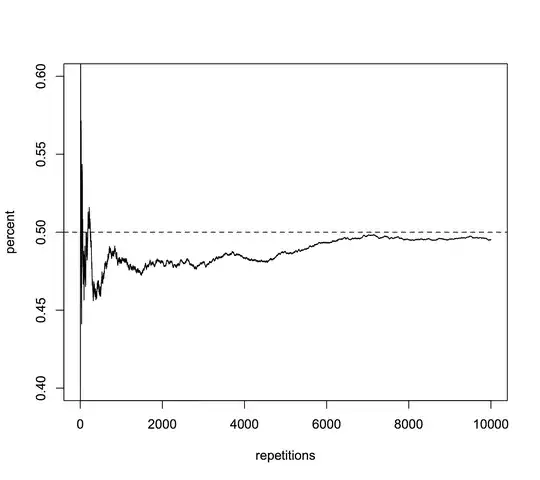
As you can see, the simulation converges close to 0.50 at around 7000 trials which may or may not be good enough for a certain application. Ultimately, you'll have to decide how close to the real world system your simulation needs to be, but assessing convergence by plotting number of simulations to the mean of the estimate (or whatever statistic you're interested in) is a means to make an informed decision.
