Like I mentioned in the comments, all I am trying suggests that what you are suggesting actually does work.
As you mentioned, intuitively it makes sense if this would work, if $X_i$ represents the posterior draw for some probability $p_i$ for event $i$ happening, you should indeed be able to sum multiple $X_i$ to get the probability of multiple events $i$, if there is no possibility of both events happening at the same time. Since this is a multinomial setting, this is not the case, so we're good.
So let's show my simulations:
library('gtools')
K <- 10
alpha <- c(rpois(K, 50)) #randomly generated alphas, just cause
k <- 2 # the number of alphas we are summing together
sim <- rdirichlet(10000, alpha)
plot(density(rowSums(sim[, 1:k]))) # the density of the summed variable
lines(density(rdirichlet(10000, c(sum(alpha[1:k]), alpha[-(1:k)]))[,1]), col = 'blue')
# the density of the variable drawn from the Dirichlet distribution with summed alphas
Let's start with $\alpha = \{10, 10, 10\}$. Summing $\alpha_1$ and $\alpha_2$ should get us $Dir(2, \{20, 10\})$:
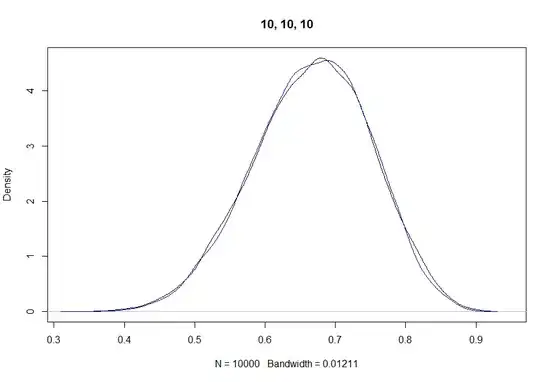
These marginal densities look pretty similar. According to wikipedia and this random lecture I found on the internet (through wikipedia), the marginal distribution of $X_i$ to the Dirichlet distribution is as follows:
$$X_i = Beta(\alpha_i, \sum_{k=1}^K\left[\alpha_k\right] - \alpha_i)$$
This relies on actually the same principle: summing all the $\alpha$ that are not $\alpha_i$ together, turning the corresponding multinomial to a binomial distributions with the outcomes $i$ and $not\textrm{-}i$. And indeed, if we fit the marginal distribution we would expect from the sum over the density in the previous picture, we see that it looks the same:
So theoretically, we should be able to take a Dirichlet distribution with a high $K$, sum all but one together and end up with a Beta distribution. Heck, let's try:
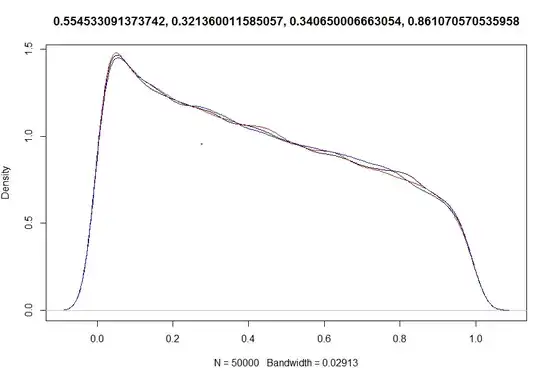
 (99 times $\alpha \sim Pois(50)$ and 1 $\alpha = 1000$, summing together the random $\alpha\mathrm{s}$.)
(99 times $\alpha \sim Pois(50)$ and 1 $\alpha = 1000$, summing together the random $\alpha\mathrm{s}$.)
To show that it also works for the joint densities, this is an example with $K=4$ and $\alpha = \{10,10,10,10\}$:
And this is with $K=3$ and $\alpha=\{20,10,10\}$:
$$\ddot{\smile}$$
So where does the confusion about $x_1^{\alpha_1-1}x_2^{\alpha_2-1}\neq (x_1 + x_2)^{\alpha_1+\alpha_2 -1 }$ come from?
Because when we sum $x_1$ and $x_2$ together, we don't just care about the density at $x_1$ and $x_2$, but for any combination of two $x$ that sums to $x_1+x_2$. I am not that strong in integration, so I'll not try and burn myself with that, but I really suggest reading this (page 3-4) for more information.
EDIT:
As @whuber correctly remarked, here is an example with low alphas, $K=4$, summing the first two $X_1$ and $X_2$: