Let's ignore the mean-centering for a moment. One way to understand the data is to view each time series as being approximately a fixed multiple of an overall "trend," which itself is a time series $x=(x_1, x_2, \ldots, x_p)^\prime$ (with $p=7$ the number of time periods). I will refer to this below as "having a similar trend."
Writing $\phi=(\phi_1, \phi_2, \ldots, \phi_n)^\prime$ for those multiples (with $n=10$ the number of time series), the data matrix is approximately
$$X = \phi x^\prime.$$
The PCA eigenvalues (without mean centering) are the eigenvalues of
$$X^\prime X = (x\phi^\prime)(\phi x^\prime) = x(\phi^\prime \phi)x^\prime = (\phi^\prime \phi) x x^\prime,$$
because $\phi^\prime \phi$ is just a number. By definition, for any eigenvalue $\lambda $ and any corresponding eigenvector $\beta$,
$$\lambda \beta = X^\prime X \beta = (\phi^\prime \phi) x x^\prime \beta = ((\phi^\prime \phi) (x^\prime \beta)) x,\tag{1}$$
where once again the number $x^\prime\beta$ can be commuted with the vector $x$. Let $\lambda$ be the largest eigenvalue, so (unless all time series are identically zero at all times) $\lambda \gt 0$.
Since the right hand side of $(1)$ is a multiple of $x$ and the left hand side is a nonzero multiple of $\beta$, the eigenvector $\beta$ must be a multiple of $x$, too.
In other words, when a set of time series conforms to this ideal (that all are multiples of a common time series), then
There is a unique positive eigenvalue in the PCA.
There is a unique corresponding eigenspace spanned by the common time series $x$.
Colloquially, (2) says "the first eigenvector is proportional to the trend."
"Mean centering" in PCA means that the columns are centered. Since the columns correspond to the observation times of the time series, this amounts to removing the average time trend by separately setting the average of all $n$ time series to zero at each of the $p$ times. Thus, each time series $\phi_i x$ is replaced by a residual $(\phi_i - \bar\phi) x$, where $\bar\phi$ is the mean of the $\phi_i$. But this is the same situation as before, simply replacing the $\phi$ by their deviations from their mean value.
Conversely, when there is a unique very large eigenvalue in the PCA, we may retain a single principal component and closely approximate the original data matrix $X$. Thus, this analysis contains a mechanism to check its validity:
All time series have similar trends if and only if there is one principal component dominating all the others.
This conclusion applies both to PCA on the raw data and PCA on the (column) mean centered data.
Allow me to illustrate. At the end of this post is R code to generate random data according to the model used here and analyze their first PC. The values of $x$ and $\phi$ are qualitatively likely those shown in the question. The code generates two rows of graphics: a "scree plot" showing the sorted eigenvalues and a plot of the data used. Here is one set of results.
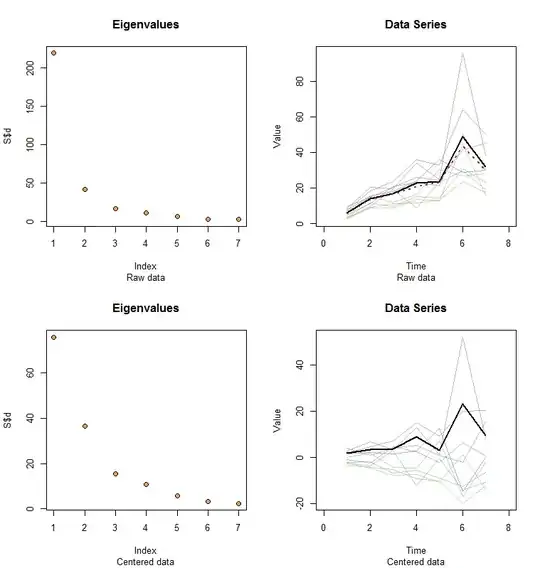
The raw data appear at the upper right. The scree plot at the upper left confirms the largest eigenvalue dominates all others. Above the data I have plotted the first eigenvector (first principal component) as a thick black line and the overall trend (the means by time) as a dashed red line. They are practically coincident.
The centered data appear at the lower right. You now the "trend" in the data is a trend in variability rather than level. Although the scree plot is far from nice--the largest eigenvalue no longer predominates--nevertheless the first eigenvector does a good job of tracing out this trend.
#
# Specify a model.
#
x <- c(5, 11, 15, 25, 20, 35, 28)
phi <- exp(seq(log(1/10)/5, log(10)/5, length.out=10))
sigma <- 0.25 # SD of errors
#
# Generate data.
#
set.seed(17)
D <- phi %o% x * exp(rnorm(length(x)*length(phi), sd=0.25))
#
# Prepare to plot results.
#
par(mfrow=c(2,2))
sub <- "Raw data"
l2 <- function(y) sqrt(sum(y*y))
times <- 1:length(x)
col <- hsv(1:nrow(X)/nrow(X), 0.5, 0.7, 0.5)
#
# Plot results for data and centered data.
#
k <- 1 # Use this PC
for (X in list(D, sweep(D, 2, colMeans(D)))) {
#
# Perform the SVD.
#
S <- svd(X)
X.bar <- colMeans(X)
u <- S$v[, k] / l2(S$v[, k]) * l2(X) / sqrt(nrow(X))
u <- u * sign(max(X)) * sign(max(u))
#
# Check the scree plot to verify the largest eigenvalue is much larger
# than all others.
#
plot(S$d, pch=21, cex=1.25, bg="Tan2", main="Eigenvalues", sub=sub)
#
# Show the data series and overplot the first PC.
#
plot(range(times)+c(-1,1), range(X), type="n", main="Data Series",
xlab="Time", ylab="Value", sub=sub)
invisible(sapply(1:nrow(X), function(i) lines(times, X[i,], col=col[i])))
lines(times, u, lwd=2)
#
# If applicable, plot the mean series.
#
if (zapsmall(l2(X.bar)) > 1e-6*l2(X)) lines(times, X.bar, lwd=2, col="#a03020", lty=3)
#
# Prepare for the next step.
#
sub <- "Centered data"
}