Premise: I have read all the stackexchange posts and other material I could find on the subject of outliers, I know Dixon, Grubbs tests, Cook's confidence or DFITS, I know the issues with non-normally distributed data, etc., so in short I kind of know what is the "consensus" on the topic of outliers detection and outliers removal.
I have valid reasons to want to remove the outliers in the specific model/context I am working on. In fact I would say that the model I am working on requires to remove the outliers, to work more safely (including the outliers creates a "too optimistic" prediction of Y based on X).
So, I am not discussing if removing outliers is good or not and I am not asking what are some good methods to detect outliers. I am proposing a specific method that I explain below, to see if it is valid and/or acceptable.
Here is my question: since we know that there are many methods that have been proposed to detect outliers, I am wondering if the follow is acceptable from a scientific point of view.
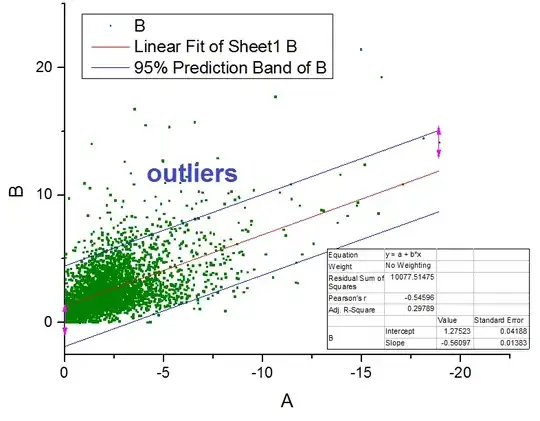
I am working on a Scatterplot like the one below, non-normal data, and assuming my model is well explained by a linear regression, if I plot Prediction Bands (95% confidence level), if I look at the blue Upper Prediction Band, it filters out a part of the data that I would be happy to call outliers and remove it, and then recalculate the linear regression on the data without the outliers.
The procedure it's performed only once to remove the outliers with the Prediction Bands and then the regression is recalculated on the new data, end of procedure.
I would like to know if any of you has ever seen this method used before, and if it is acceptable or valid to detect and remove outliers, starting from the assumption that we want/need to remove the outliers to make the model "safer" in the prediction of Y.