Is my data time dependent?

Question

I have the following linear model on running data recorded on a running app: $Y$ is the avg speed of the run, $X_1,\ldots, X_4$ are the distance ran, elevation gain during run, and temperature and humidity at the start of the run, and also $M$ which counts time difference (in months) between the start date of the run and today's date. I was not expecting $M$ to be treated as a "time component," but from my observations it seems like it makes the sample "time series" data. This is being posted because my understanding of time series is questionable.

The fitted model is a standard linear regression $$LM01: Y=\beta_0+\beta_1M+\sum_{i=2}^5\beta_iX_{x-1}.$$ From this model the residuals are normally distributed, but I find that they are autocorrelated from the following two tests:

    > dwtest(lm(average_speed~., data = trainData))

    Durbin-Watson test

    data:  lm(average_speed ~ ., data = trainData)
    DW = 0.96952, p-value = 1.233e-07
    alternative hypothesis: true autocorrelation is greater than 0

    > resModel = lm(res[-length(res)] ~ res[-1])
    > summary(resModel)

    Call:
    lm(formula = res[-length(res)] ~ res[-1])

    Residuals:
         Min       1Q   Median       3Q      Max 
    -2.84748 -0.36145  0.09688  0.45663  1.65230 

    Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
    (Intercept)  0.02137    0.08280   0.258    0.797    
    res[-1]      0.50359    0.09803   5.137 2.05e-06 ***

Also the ACF and PACF plots from the residuals. At this point, this autocorrelation is not a bad thing right? or is it? From what I understand, if we want to see if we have time dependent data we should first ignore the time component and see if there is autocorrelation in the residuals. Only then may we conclude that there needs to be some adjustment for the time component.

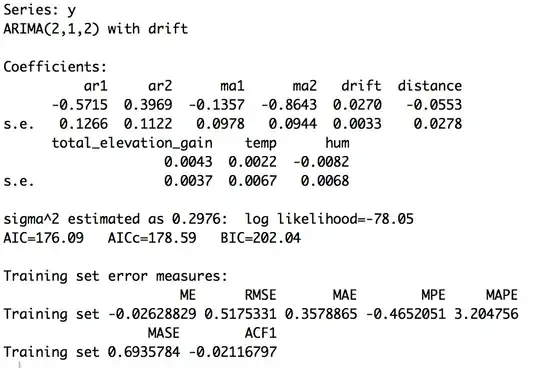
That is, we should fit $$LM02: Y=\beta_0+\sum_{i=1}^4\beta_iX_{x}$$ and test for the autocorrelation of the residuals. The residuals are normally distributed and I did the same two tests as above and the conclusions are the same. Additionally, the ACF plot and the PACF plot look worse. Now, it is from this test that we may conclude that some time component needs to be accounted for (say like an ARM model). Is this conclusion correct?

Additionally, the Months variable $M$ was featurized from date data. If $M$ is to be a time component would it be better if it is counted in days?

Also, is there another way to circumvent the autocorrelation problem? Like using some regularization technique? Or is time series the only way to go from here?

Thanks in advance.

Edit:

Answer 1

Well, given that your series is using dates, i.e. measuring data between the start date and today’s date, then it is a time series analysis.

Regarding autocorrelation, this is a characteristic of time series models. However, if you were using OLS, then autocorrelation is a violation of the assumption that OLS is BLUE (Best Linear Unbiased Estimator).

One possible way to remedy this is by using the Cochrane-Orcutt method and see what your results generate:

install.packages('orcutt')
library(orcutt)
resModel2 <- cochrane.orcutt(resModel)
resModel2

However, given that you seem to have one variable in your model, average speed, then it is likely preferable to use a strictly time-series based model such as ARIMA or Holt-Winters to conduct forecasts on the basis of current data. I am not sure what type of results your ACF/PACF plots are generating, but one possibility could be to use the auto.arima() function to determine the best (p,d,q) order automatically, i.e. where p is the number of time lags of the autoregressive model, d is the level of differencing, and q is the moving average term.