35

Let's say I have a model that gives me projected values. I calculate RMSE of those values. And then the standard deviation of the actual values.

Does it make any sense to compare those two values (variances)? What I think is, if RMSE and standard deviation is similar/same then my model's error/variance is the same as what is actually going on. But if it doesn't even make sense to compare those values then this conclusion could be wrong. If my thought is true, then does that mean the model is as good as it can be because it can't attribute what's causing the variance? I think that last part is probably wrong or at least needs more information to answer.

jkim19
  • 451
  • 1
  • 4
  • 3

3 Answers3

32

Let's say that our responses are $y_1, \dots, y_n$ and our predicted values are $\hat y_1, \dots, \hat y_n$.

The sample variance (using $n$ rather than $n-1$ for simplicity) is $\frac{1}{n} \sum_{i=1}^n (y_i - \bar y)^2$ while the MSE is $\frac{1}{n} \sum_{i=1}^n (y_i - \hat y_i)^2$. Thus the sample variance gives how much the responses vary around the mean while the MSE gives how much the responses vary around our predictions. If we think of the overall mean $\bar y$ as being the simplest predictor that we'd ever consider, then by comparing the MSE to the sample variance of the responses we can see how much more variation we've explained with our model. This is exactly what the $R^2$ value does in linear regression.

Consider the following picture: The sample variance of the $y_i$ is the variability around the horizontal line. If we project all of the data onto the $Y$ axis we can see this. The MSE is the mean squared distance to the regression line, i.e. the variability around the regression line (i.e. the $\hat y_i$). So the variability measured by the sample variance is the averaged squared distance to the horizontal line, which we can see is substantially more than the average squared distance to the regression line. 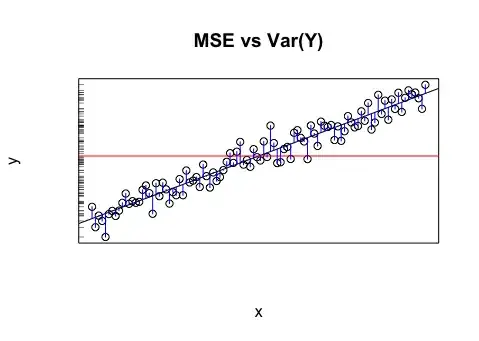enter image description here

jld
  • 18,405
  • 2
  • 52
  • 65
  • If (n-1) should be used for the sample variance, does that mean that, for the sake of this comparison, the MSE should also be computed using (n-1)? – rvbarreto Apr 09 '20 at 07:40
  • @rvbarreto I don't see MSE with $n-1$ since the degrees of freedom in $\hat y$ are more complicated but in general that's all just about scaling factors and doesn't affect the key ideas – jld Apr 09 '20 at 22:10
22

In the absence of better information, the mean value of the target variable can be considered a simple estimate for values of the target variable, whether in trying to model the existing data or trying to predict future values. This simple estimate of the target variable (that is, predicted values all equal the mean of the target variable) will be off by a certain error. A standard way to measure the average error is the standard deviation (SD), $ \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - \bar y)^2}$, since the SD has the nice property of fitting a bell-shaped (Gaussian) distribution if the target variable is normally distributed. So, the SD can be considered the amount of error that naturally occurs in the estimates of the target variable. This makes it the benchmark that any model needs to try to beat.

There are various ways to measure the error of a model estimation; among them, the Root Mean Squared Error (RMSE) that you mentioned, $ \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - \hat y_i)^2}$, is one of the most popular. It is conceptually quite similar to the SD: instead of measuring how far off an actual value is from the mean, it uses essentially the same formula to measure how far off an actual value is from the model's prediction for that value. A good model should, on average, have better predictions than the naïve estimate of the mean for all predictions. Thus, the measure of variation (RMSE) should reduce the randomness better than the SD.

This argument applies to other measures of error, not just to RMSE, but the RMSE is particularly attractive for direct comparison to the SD because their mathematical formulas are analogous.

Edit:

Someone asked me offline for a citation that supports the idea of the SD being a benchmark for the RMSE. Personally, I first learnt this principle from Shmueli et al. 2016. Sorry, but I do not have the book handy, so I cannot cite a page number.

Shmueli, G., Bruce, P. C., Stephens, M., & Patel, N. R. (2016). Data Mining for Business Analytics: Concepts, Techniques, and Applications with JMP Pro (3rd Edition). Wiley.

Tripartio
  • 1,517
  • 1
  • 13
  • 19
  • This is the best answer because it explains how the comparison might be useful rather than just describing the differences. – Hans Nov 14 '19 at 15:40
7

In case you are talking about the mean squared error of prediction, here it can be: $$ \frac{\sum_i(y_i-\hat{y}_i)^2}{n-p}, $$ depending on how many (p) parameters are estimated for the prediction, i.e., loss of the degree of freedom (DF).

The sample variance can be: $$ \frac{\sum_i(y_i - \bar{y}) ^2}{n-1}, $$ where the $\bar{y}$ is simply an estimator of the mean of $y_i$.

So you can consider the latter formula (sample variance) as a special case of the former (MSE), where $\hat{y}_i = \bar{y}$ and the loss of DF is 1 since the mean computation $\bar{y}$ is an estimation.

Or, if you do not care much about how $\hat{y}_i$ is predicted, but want to get a ballpark MSE on your model, you can still use the following formula to estimate it, $$ \frac{\sum_i(y_i-\hat{y}_i)^2}{n}, $$

which is the easiest to compute.

Xiao-Feng Li
  • 531
  • 5
  • 7
  • 1
    I have no privilege to comment on @Chaconne 's answer, but I doubt if his last statement has a typo, where he says: "So the variability measured by the sample variance is the averaged squared distance to the horizontal line, which we can see is substantially less than the average squared distance to the line". But in the figure in his answer, the prediction of the y values with the line is pretty accurate, which means the MSE is small, at least much better than the "prediction" with a mean value. – Xiao-Feng Li Mar 20 '17 at 02:00