2

Is it reasonable to choose a regression model with a value of 0 for the intercept when this makes logical sense? For example, I am trying to model a physical geometric relationship, and I know that when x = 0, y = 0. Yet the consequences of choosing such a model are that the R^2 value becomes significantly higher (it changes from 0.67 to 0.95). When I examine the residuals for both models, I can see that they both have roughly the same distribution. The origin option is shown in Figure 1 and non-origin in Figure 2.

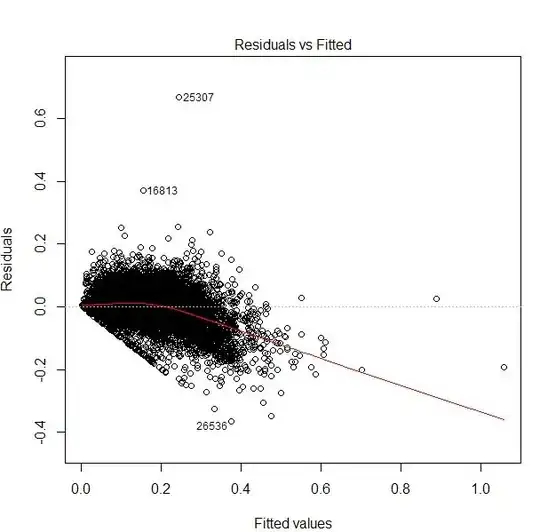
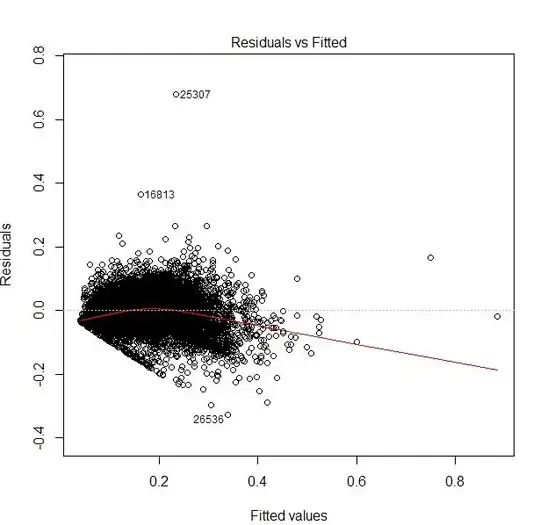
enter image description here

enter image description here

How should I decide which model is more appropriate?

I've read through some of the other questions and answers on this topic but I haven't seen any discussion about physical limitations providing the basis for the choice.

My dependent variable here is an area calculation, and my independent variable is a measurement of one dimension of the shape. For example, if I had a set of rectangles of length l, width w and area A, I am trying to model the relationship between l and A. However, as these are not perfectly regular there is some variation in the relationship but it appears to be linear in several cases, and based on some of the comments, not so much in this particular instance.

Community
  • 1
celenius
  • 1,324
  • 4
  • 15
  • 26
  • 2
    Both models seem to have a problem - there are some fitted values that are much higher than all the others, and there are some outliers. Can you tell us what you are trying to do? What is the DV and the IVs? – Peter Flom Mar 07 '12 at 18:27
  • @PeterFlom and hetereoscedasticity too. – Michelle Mar 07 '12 at 18:56
  • Remember that in R, the denominator of R-squared changes when you don't fit an intercept: http://stat.ethz.ch/R-manual/R-patched/library/stats/html/summary.lm.html . So R-squared values for models with and without an intercept aren't comparable. – onestop Mar 07 '12 at 19:52
  • @onestop, what do you mean that they are not comparable? I just read through the link and did not understand what you meant. – celenius Mar 07 '12 at 20:07
  • @PeterFlom I just updated my question a little more. I hope that clarifies the context a little. – celenius Mar 07 '12 at 20:18
  • 1
    R-squared is the proportion of 'total variance' explained. Usually, 'total variance' is the sum of squares of the y values *about their mean*. But if you don't fit an intercept, it's the sum of squares of the y values, which will be higher (unless the mean of the y values is exactly zero). – onestop Mar 07 '12 at 20:30
  • 4
    Celenius, I believe this question *is* answered in other threads, but consider this example. Suppose you are modeling areas of rectangles, but the shapes in your dataset are not arbitrary: when a rectangle has width $w \le 1$, its length will be $4/w-3$. Regressing area on $w$ gives area = $4-3w$, with an important non-zero intercept, even though for geometrical reasons all rectangles of width $0$ have area $0$. The point is that the value of the dependent variable at $0$ *does not matter*: you need to consider the *limiting* value as the independent variable approaches $0$. – whuber Mar 07 '12 at 20:41
  • if you have than 10,000 dimensions, having a bias or not doesn't really matter. – Charlie Parker Feb 02 '17 at 21:00

0 Answers0