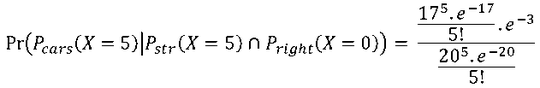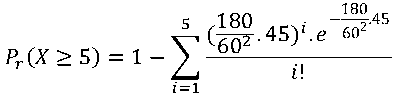Hi So I have this question below. I know I need to model each lane as a separate Poisson distribution. The possible answers are:
a) 11.4%; 22.4%; 33.4%; 44.4%; 55.4%
b) 2.74%; 4.74%; 12.74%; 34.74%; 64.74%
but obviously I need to know how to get to the answer.
Question:
Vehicles arrive at a rate of $1200$ vehicles per hour at a traffic signal. $15\%$ of the vehicles turn right while $85\%$ travel straight through. The street has one lane per direction, which is widened at the intersection to one straight through lane, and one right-turn lane. The right-turn lane can accommodate $5$ vehicles but will be blocked if $5$ or more straight-through vehicles are waiting at the intersection. Determine the following:
a) The probability that no vehicles are waiting in the right-turn lane while there is a total of $5$ vehicles waiting at the intersection.
b)The probability that more than $5$ right-turn vehicles will arrive at the intersection during the next red period of $45$ seconds.
For question a) I think I need to find $\Pr(X=5)$ for the straight lane while $\Pr(X=0)$ for the right lane. $$ \Large P_P(x; qt) = \frac{(q\cdot t)^x\cdot e^{-q\cdot t}}{x!} $$
Where I am having trouble though is how do I determine $q$?