This question appears to use some statistical terminology in unconventional ways. Understanding this will help resolve the issues:
A "signal" appears to be a (measurable) function $x$ defined on a determined Real interval $[t_-, t_+)$. (This makes $x$ a random variable.) That interval is endowed with a uniform probability density. Taking $t$ as a coordinate for the interval, the probability density function therefore is $\frac{1}{t_+-t_-} dt$.
A "sample" of a signal is a sequence of values of $x$ obtained along an arithmetic progression of times $\ldots, t_0 - 2h, t_0-h, t_0, t_0+h, t_0+2h, \ldots$ = $(t_1,t_2,\ldots,t_n)$ (restricted, of course, to the domain $[t_-, t_+)$). These values may be written $x(t_i) = x_i$.
The "expectation" operator $E$ may refer either to (a) the expectation of the random variable $x$, therefore equal to $\frac{1}{t_+-t_-}\int_{t_-}^{t_+}x(t)dt$ or (b) the mean of a sample, therefore equal to $\frac{1}{n}\sum_{i=1}^n x_i$. This lets us translate formulas for expectations of signals to formulas for expectations of their samples merely by replacing integrals by averages.
"Statistical independence" of signals $x$ and $y$ means they are independent as random variables.
The importance of powers of $\sin$ and $\cos$ becomes evident when we notice that "most" signals can be written as convergent Fourier series -- that is, linear combinations of the functions $\sin(n t)$, $n=1, 2, \ldots$, and $\cos(m t)$, $m=0, 1, 2, \ldots$, and that these functions, in turn, can be written as (finite) linear combinations of non-negative integral powers of products, $\sin^p(t)\cos^q(t)$. Because the expectation operator is linear, we would naturally be interested in studying and computing expectations of such monomials.
Now, $\sin$ and $\cos$ are usually not "statistically independent" except when the length of the interval, $t_+ - t_-$, is a multiple of $2\pi$. The signals of interest in applications are those for which this length is huge. Thus, at least to a very good approximation, we can think of $\sin$ and $\cos$ as being independent. But what does this mean? How can we think about it?
To discuss the concepts, I am going to make an "ink = probability" metaphor by considering scatterplots of large independent samples of $(x,y)$. If $A$ is any (measurable) region within the scatterplot, then the proportion of ink covering $A$ closely approximates the probability of $A$ under the joint distribution of $(x,y)$.
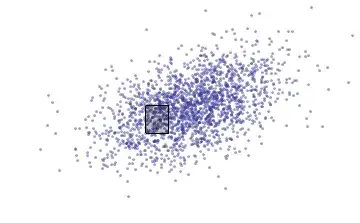
$x$ is plotted on the horizontal axis and $y$ on the vertical. $A$ is the rectangle. The proportion of blue ink drawn on this rectangle equals the proportion of the 2000 dots used, which reflect the joint probability density of $(x,y)$.
The statistical definition of independence of two random variables $x$ and $y$ is that their joint distribution is the product of the marginal distributions. The marginal distribution of $x$ is obtained by taking thin vertical slices of the scatterplot: the chance that $x$ lies between $x'$ and $x'+dx$ equals the proportion of ink used for all points in this region, regardless of the value of $y$: that's a vertical strip.
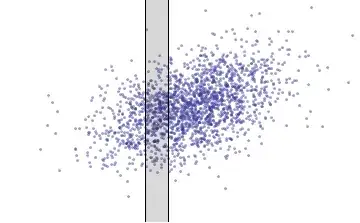
Now, in any vertical strip, some of the ink appears more in some places than in others. Compare these two strips:
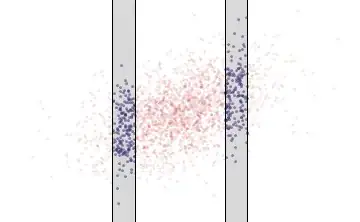
In the right-hand strip in this illustration, the blue ink tends to be higher (have larger $y$ values) than in the left-hand strip. This is lack of independence. Independence means that no matter where the strip is located, you see the same vertical distribution of ink, as here:

What is interesting about this last figure is how it was drawn. It is a scatterplot of a sample $(x(t), y(t))$ at 10,000 equally spaced times. Let's look at the first one percent of this sample:

There is a clear lack of independence here! During any small interval of time, two signals can be highly functionally dependent, but if over a long period of time that functional dependence "averages out," the signals are still considered independent. (In this case the signals were $x(t) = \cos((e/20)t)$ and $y(t) = \sin(t/20)$ sampled at times $t=1, 2, \ldots, 10000$.)
Let's get back to the questions, which concern expectation as well as independence. We can also think of expectation geometrically: in a scatterplot of two signals (or their samples), $(x,y)$, $E[x]$ is the average horizontal location of the dots and $E[y]$ is the average vertical location. For instance, consider the signals $x(t)=\cos(t)$ and $y(t)=\sin(t)$ over the interval $[0, 2\pi)$, with this scatterplot:
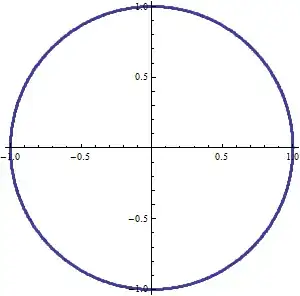
The symmetrical form indicates the average of $x$ must be at $0$ and likewise for the average of $y$. Therefore $E[\cos(t)]$ = $E[\sin(t)]$ = $0$ (for this particular domain).
Consider now their squares. Here's the scatterplot:
Of course! $\cos^2(t) + \sin^2(t)=1$, so the squares must lie along the line $x+y=1$. The average of each coordinate is $1/2$. Naturally the averages cannot be zero: squares tend to be positive. So, if we wish to find the second central moment of (say) $x(t) = cos^2(t)$, often written $\mu'_2(x)$, then we first compute its expectation ($1/2$) and (by definition) integrate the second power of the residuals:
$$\mu'_2(x) = E[(x - E[x])^2] = \frac{1}{t_+ - t_-}\int_{t_-}^{t_+}\left(\cos^2(t) - 1/2\right)^2 dt.$$
In general, the $(p,q)$ central moment of a bivariate signal $(x,y)$, written $\mu'_{pq}(x,y)$, is obtained similarly: first compute the expectations of $x$ (written $\mu(x)$) and $y$ (written $\mu(y)$), and then find the expectation of the appropriate monomial in the residuals $x(t) - \mu(x)$ and $y(t) - \mu(y)$:
$$\mu'_{pq}(x,y) = \frac{1}{t_+-t_-}\int_{t_-}^{t_+}\left(x(t)-\mu(x))^p\right)\left(y(t)-\mu(y)\right)^q dt.$$
Continuing the example posed in the question, let $x(t) = \sin(t)$, $y(t) = \cos(t)$, and suppose the domain is a multiple of one common period of both signals; say, $[t_-, t_+)$ = $[0, 2\pi)$. As we have seen, $\mu(x)$ = $\mu(y)$ = 0. Therefore
$$\mu'_{23}(x,y) = \frac{1}{2\pi}\int_0^{2\pi}\left(\sin(t)-0\right)^2\left(\cos(t)-0\right)^3dt = 0.$$
More generally (in this case) $\mu'_{2m,2n}(x,y) = \frac{\pi ^{1/2} 2^{m+2 n-1}}{\Gamma \left(\frac{1}{2}-n\right) \Gamma \left(-m-n+\frac{1}{2}\right) \Gamma (2 m+2 n+1)}$ for non-negative integral $m,n$; all other central moments are zero. (This formula in terms of Gamma functions works for non-integral $m$ and $n$.)
A subtle and potentially confusing point concerns what we consider $x$ to be. If, instead of taking $x(t)=\sin(t)$, we consider the different signal $x(t)=\sin^2(t)$, then, as we have seen, $\mu(x)=1/2$ and therefore
$$\mu'_2(x) = \mu'_2(\sin^2(t)) = \frac{1}{2\pi}\int_0^{2\pi}\left(\sin^2(t)-1/2\right)^2 dt = 1/8.$$
Beware: because the expectation of $\sin^2$ is nonzero, its second central moment, $1/8$, does not necessarily equal the fourth central moment of $\sin$ (which equals $3/8$), even though both integrals involve fourth powers of $\sin$.
Finally, when working with samples, just replace the integrals by averages.






