3

Suppose I have $m$ individuals from a population (not necessarily people: here "individuals" may also indicate machines of common design). $m$ is small, say, 10. For each individual I measure some quantity as a function of time: the number of time observations (the sample size) is different for each individual, i.e., $N_1,\dots, N_m$. EDIT: the sampling rate is the same for all individuals.

The quantity in question doesn't (seem to) exhibit some trend: it randomly oscillates around the time mean, which may differ from individual to individual, with a standard deviation which is roughly constant with time (for a given individual). Just to be clear, the oscillation doesn't seem to be harmonic: it's random, but its amplitude doesn't seem to depend on time.

I have two goals:

  • I want to estimate the time mean and standard deviation of the population. How do I combine the time series from the different individuals to do that? Do I need to take into account the different sample sizes, and if so, how?
  • I want to estimate the time mean and standard deviation for a new individual, not observed. In other words, I would like to compute a prediction interval for the time mean and the time standard deviation. How do I do that with time series?

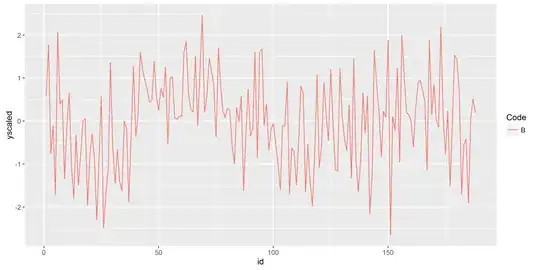
EDIT: here is a plot of a single time series for one individual.

enter image description here

Looking at the standardized time series, it could seem that the variation is not small. However, consider that the oscillation is much smaller than the time average: I cannot show the actual values, but for each individual $j$ the sample coefficient of variation

$$V_j =\frac{\bar{X}_j}{S_j} \approx 6 \cdot 10^{-4} $$

where with $\bar{X}_j$ and $S_j$ I denote

$$\bar{X}_j = \frac{\sum_{i=1}^{N_j} X_{ij} }{N_j}, \quad S_j =\sqrt{ \frac{ \sum_{i=1}^{N_j} (X_{ij}-\bar{X}_j)^2 }{ N_{j-1} } } $$

EDIT2: following GeoMat22's comments, I understand that I could compute $\bar{X}_1,\dots,\bar{X}_m$ and $\frac{S_1}{n_{eff,1}},\dots,\frac{S_m}{n_{eff,m}}$ for each individual. I still miss two steps: how to compute in practice $n_{eff,j}$ for each individual, and how to combine all these data to get an estimate and a standard error for 1) the time mean of the population and 2) the time mean of a new, unobserved, individual.

DeltaIV
  • 15,894
  • 4
  • 62
  • 104
  • So to clear, it seems that every individual has a mean and a standard deviation and that each measurement for a given individual is an IID random variable? – dimpol Oct 25 '16 at 06:39
  • No, I don't think each measurement is IID. But the correlation length seems to be short, and the process to be (or tend asymptotically to be) stationary. I need time to anonymize the data, but I'll put some plots in the afternoon. – DeltaIV Oct 25 '16 at 06:42
  • Are the measurements of different individuals dependent on each other? – dimpol Oct 25 '16 at 06:55
  • No, you can safely assume they're not. The individuals come from a common population, but each individual is measured independently of the other individuals. – DeltaIV Oct 25 '16 at 08:48
  • I added the plot as promised. – DeltaIV Oct 25 '16 at 12:42
  • How do you define the mean and the standard deviation of the population? Are you looking at the sum of a single measurement of each individual and then the properties of that sum? Or just the mean of the means of each individual? – dimpol Oct 25 '16 at 13:07
  • 1
    You should probably change the plot to be either 1) a single time series for one individual, or 2) time series of the same attribute for several individuals. Showing multiple attributes for the same individual is not helpful, as you say this is not your question, but it may confuse people. **Question:** My first thought is to consider something like [this](http://stats.stackexchange.com/a/73145) to account for "effective sample size" due to autocorrelation. You say $\Delta{t}$ is constant while $n_t$ varies across individuals, but does $\tau_{\mathrm{corr}}$ vary also? – GeoMatt22 Oct 25 '16 at 13:32
  • @GeoMatt22, You're right, the multiple attributes generate confusion, I will fix the plot. I got a little carried away by thinking to my final goal, which actually involves predicting not a single mean/sd for a new individual, but a spatial function with uncertainty bars for a new individual....you probably recall [this question](http://stats.stackexchange.com/questions/234785/regression-on-the-unit-disk-starting-from-uniformly-spaced-samples). Concerning your **question**, I don't know. I can compute the autocorrelation function for different individuals, but I have little familiarity [1/2] – DeltaIV Oct 25 '16 at 15:43
  • [2/2] with the concept, and I lack the experience to judge if the difference in autocorrelation functions is "significant". – DeltaIV Oct 25 '16 at 15:46
  • 1
    I also do not have much experience with autocorrelation significance. But the main idea is 1) if you had i.i.d. data you could do your calculation easily, so 2) can the time series be treated as "i.i.d. samples" for some "effective sample size"? ($\tau$ could vary between series I guess, although if it did this might cast doubt on the "ensemble stationarity" assumption?) – GeoMatt22 Oct 25 '16 at 15:59
  • This concept of effective sample size you linked to, seems spot on. I'll study it and see what I can get. Thanks! – DeltaIV Oct 25 '16 at 16:07

0 Answers0