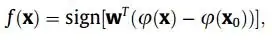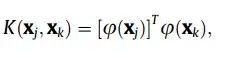I'm trying to implement a paper that used SVM and an improve of it with Bayesian decision theory. How do I do the mapping feature $\phi(x)$ that appears in the decision function?
The paper used an RBF kernel, I have the kernel from the Mercer, with the inner product of the vector x.
But I do not understand how to do the function $\phi(x)$.
$\phi(x)$ is implied by the kernel $k$. So, in general, you don't have access to $\phi$. This is a remarkable property of kernels. For example, the popular RBF kernel has a corresponding $\phi$ that is infinite dimensional (and so cannot be computed directly).
You might have a hard time improving the SVM with anything Bayesian... the magic of the SVM is that the optimization reduces $\phi$ to computing inner products in the reproducing kernel Hilbert space implied by $\phi$... Thus, you never have to calculate $\phi$, which is usually computationally intractable. That said, you can use your Bayesian methods with most convex non-linearities (and just put that in place of $\phi$). But be aware that the computational complexity tends explode... Or you could just do the whole neural network thing and throw convexity out the window and learn $\phi$ (i.e., the neural network).
