3

If $\mathbf{Cov}=0$ let $u=x \cdot cos(\theta)+y \cdot sin(\theta)$

and $v =y \cdot cos(\theta)-x \cdot sin(\theta)$.

What will be $\mathbf{Cov}(u,v)$? Will it be $0$?

Firebug
  • 15,262
  • 5
  • 60
  • 127
Sumedha ghosh
  • 31
  • 2
  • Is this [tag:self-study]? Please read the tag description, and if it fits, please add the tag. Otherwise ignore, thanks. – Firebug Oct 19 '16 at 12:53

1 Answers1

4

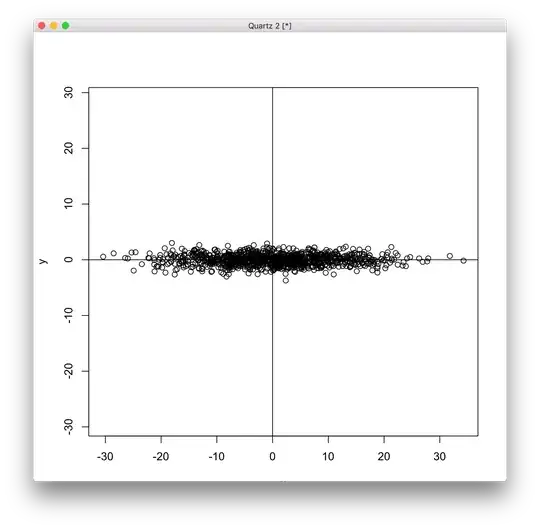
Firstly a quick empirical example to get an intuition. Take the x,y as in the following figure, which have a sample covariance very close to 0 (actual value -0.038): x,y with covariance 0

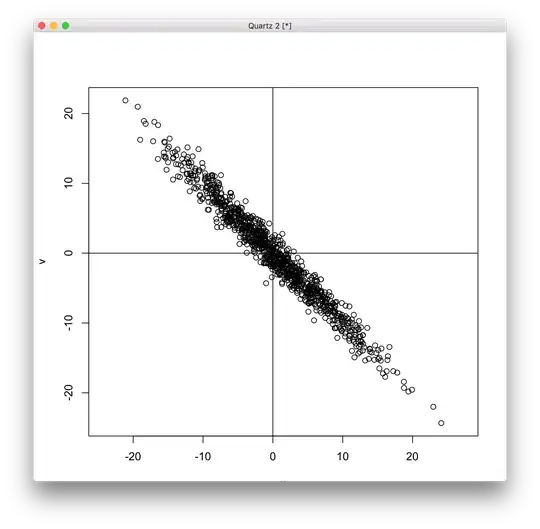
Rotate these values by 45 degrees, giving u,v in the following figure: u,v by rotating x,y 45 degrees

Do you think the correlation is still 0?

Now to the theoretical bit. Remember that the covariance is bilinear, that is $$\operatorname{cov}(x,ay + w) = a\operatorname{cov}(x,y) + \operatorname{cov}(x,w),$$

and same for the first variable.

Using this for $\operatorname{cov}(u,v)$, and using the fact that $\operatorname{cov}(x,y) = 0$, we get $$\operatorname{cov}(u,v) = \operatorname{cov}(x,x)\sin(\theta)\cos(\theta) + \operatorname{cov}(y,y)\sin(\theta)\cos(\theta)$$ $$ = [\operatorname{var}(x) + \operatorname{var}(y)]\sin(\theta)\cos(\theta)$$

which is not necessarily 0.

Lima
  • 87
  • 3
  • In fact, the covariance of the rotated variables is $0$ only when $\theta$ is a multiple of $\pi/2$ and such rotations are negations or interchange of the original variables. – Dilip Sarwate Oct 19 '16 at 16:32
  • Discarding the degenerate case, when the variances are 0, that is correct! – Lima Oct 24 '16 at 07:08